题目内容
5. 如图,在△ABC中,AB=3$\sqrt{2}$,BC=1,∠ABC=45°,以AB为边作等腰直角△ABD,使∠ABD=90°,连接CD,则线段CD的长为$\sqrt{13}$.
如图,在△ABC中,AB=3$\sqrt{2}$,BC=1,∠ABC=45°,以AB为边作等腰直角△ABD,使∠ABD=90°,连接CD,则线段CD的长为$\sqrt{13}$.
分析 延长BC交AD于点E,根据等腰直角三角形的性质求出AD,再求出BE=DE=$\frac{1}{2}$AD并得到BE⊥AD,然后求出CE,在Rt△CDE中,利用勾股定理列式计算即可得CD的长.
解答  解:延长BC交AD于点E,
解:延长BC交AD于点E,
∵∠ABD=90°,∠ABC=45°,
∴∠DBC=45°,
∵AB=BD,
∴BE=DE=$\frac{1}{2}$AD,BE⊥AD,
∵AB=3$\sqrt{2}$,
∴AD=6,
∴DE=BE=3,
∵BC=1,
∴CE=2,
∴CD=$\sqrt{D{E}^{2}+C{E}^{2}}$=$\sqrt{13}$,
故答案为:$\sqrt{13}$.
点评 本题考查了勾股定理,等腰直角三角形的性质,解题的关键是正确作出辅助线,利用等腰三角形的性质得到直角三角形.

练习册系列答案
相关题目
12.以等腰三角形底角的度数x(单位:度)为自变量,顶角的度数y为因变量的函数关系式为( )
| A. | y=180-2x(0<x<90) | B. | y=180-2x(0<x≤90) | C. | y=180-2x(0≤x<90) | D. | y=180-2x(0≤x≤90) |
17.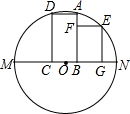 如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
 如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )
如图,矩形ABCD中,AB=2AD,A、D在半圆O上,B、C在半圆O的直径MN上,另一个矩形BFEG紧靠着矩形ABCD,F在AB上,E在半圆O上,G在直径MN上,且GE=2BG=4,则矩形ABCD的面积为( )| A. | $\frac{25}{2}$ | B. | 12 | C. | 15 | D. | $\frac{27}{2}$ |
 若将一根长10cm的细木棒放入长、宽、高分别是5cm、4cm、3cm的木箱中,求细木棒露在箱外的最短长度.(精确到0.01cm)
若将一根长10cm的细木棒放入长、宽、高分别是5cm、4cm、3cm的木箱中,求细木棒露在箱外的最短长度.(精确到0.01cm)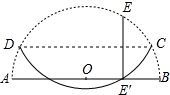 如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是2$\sqrt{3}$≤CD<4.
如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是2$\sqrt{3}$≤CD<4.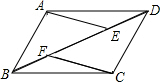 如图,在?ABCD中,点E、F在BD上,且BF=DE.
如图,在?ABCD中,点E、F在BD上,且BF=DE.