题目内容
10.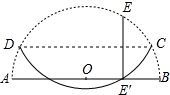 如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是2$\sqrt{3}$≤CD<4.
如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是2$\sqrt{3}$≤CD<4.
分析 由题意可知:当被折的圆弧与直径AB至少有一个交点时则被折的圆弧与直径AB相切时折痕CD的长度最短,当CD和直径重合时,折痕CD最长,由此即可折痕CD的长度取值范围.
解答 解:当被折的圆弧与直径AB至少有一个交点时则被折的圆弧与直径AB相切时折痕CD的长度最短,如图所示:
连接OD,
∵EH=OH=$\frac{1}{2}$OE=1,OD=2,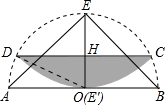
∴DH=$\sqrt{O{D}^{2}-O{H}^{2}}$=$\sqrt{3}$,
∵OH⊥DC,
∴DH=CH,
∴CD=2DH=2$\sqrt{3}$,
当CD和直径AB重合时,折痕CD最长,所以CD=4,
又因为要保证被折的圆弧与直径AB至少有一个交点,所以CD不能取到4,即CD<4,
综上可知2$\sqrt{3}$≤CD<4,
故答案为:2$\sqrt{3}$≤CD<4.
点评 本题考查了和圆有关的综合题,用到的知识点有:垂径定理、勾股定理,切线的性质定理以及折叠的性质,解题的关键是找到CD最短和最长时的位置.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 如图,在△ABC中,AB=3$\sqrt{2}$,BC=1,∠ABC=45°,以AB为边作等腰直角△ABD,使∠ABD=90°,连接CD,则线段CD的长为$\sqrt{13}$.
如图,在△ABC中,AB=3$\sqrt{2}$,BC=1,∠ABC=45°,以AB为边作等腰直角△ABD,使∠ABD=90°,连接CD,则线段CD的长为$\sqrt{13}$.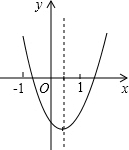 二次函数y=ax2+bx+c的图象如图所示,那么abc,b2-4ac,2a+b,a+b+c四个代数式中,值为正数的有3 个.
二次函数y=ax2+bx+c的图象如图所示,那么abc,b2-4ac,2a+b,a+b+c四个代数式中,值为正数的有3 个.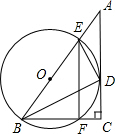 如图:在Rt△ABC中,∠C=90°,BC=9,CA=12,∠ABC的平分线BD交AC于点D,DE垂直DB于点E,点O在AB上,圆O是△BDE的外接圆,交BC于点F,连接EF,求EF:AC的值.
如图:在Rt△ABC中,∠C=90°,BC=9,CA=12,∠ABC的平分线BD交AC于点D,DE垂直DB于点E,点O在AB上,圆O是△BDE的外接圆,交BC于点F,连接EF,求EF:AC的值.