题目内容
15．
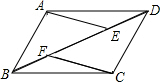如图，在?ABCD中，点E、F在BD上，且BF=DE．（1）写出图中所有你认为全等的三角形；
（2）请选择一对证明．
分析 （1）根据平行四边形的性质和BF=DE，找到全等三角形：△ABE≌△DCF；△ABD≌△DCB；△AED≌△CBF；
（2）无论哪一对全等三角形的证明过程都差不多，都利用平行四边形的性质和BF=DE来构造全等条件．
解答 解：（1）△ABD≌△CDB；△ABE≌△CDF；△ADE≌△CBF；
（2）证明△AED≌△CBF，
∵四边形ABCD是平行四边形，
∴AD=BC，∠ADB=∠BCF．
又∵BF=DE，BE-EF=DF-EF，
∴BF=DE．
在△AFD和△CBE中，
$\left\{\begin{array}{l}{AD=BC}\\{∠ADB=∠BCF}\\{DE=BF}\end{array}\right.$，
∴△AFD≌△CBE（SAS）．
（注：同样可以选择其余两对三角形证明）
点评 此题是开放性试题，要求学生对平行四边形的性质非常熟悉，只有这样才能很好发挥性质的作用，找到全等条件证明三角形全等．
练习册系列答案
相关题目
如图，在△ABC中，AB=3$\sqrt{2}$，BC=1，∠ABC=45°，以AB为边作等腰直角△ABD，使∠ABD=90°，连接CD，则线段CD的长为$\sqrt{13}$．
6．下列各数中无理数共有（ ）
$\frac{22}{7}$，-π，3.$\stackrel{••}{14}$，0.131331…（相邻二个1之间3的个数逐次加1），-$\sqrt{49}$，$\root{3}{9}$．
$\frac{22}{7}$，-π，3.$\stackrel{••}{14}$，0.131331…（相邻二个1之间3的个数逐次加1），-$\sqrt{49}$，$\root{3}{9}$．
| A． | 4个 | B． | 3个 | C． | 2个 | D． | 1个 |
如图所示，小明家到学校有3条路可走，一般情况下，小明通常走②路，其中的数学道理是两点之间，线段最短．