题目内容
12.一元二次方程x(x-2)=0的解是( )| A. | x=2 | B. | x=0 | C. | x=0或x=2 | D. | x=0或x=-2 |
分析 由两个一次式的乘积为0得出这两个一次式都可能等于0,可得关于x的一元一次方程,解之可得.
解答 解:∵x(x-2)=0,
∴x=0或x-2=0,
解得:x=0或x=2,
故选:C.
点评 本题主要考查因式分解法解一元二次方程,因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
20.估计$\sqrt{16}$+$\sqrt{20}$的运算结果应在( )
| A. | 6与7之间 | B. | 7与8之间 | C. | 8与9之间 | D. | 9与10之间 |
17. 如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
 如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )
如图所示,两个反比例函数y=$\frac{{k}_{1}}{x}$ 和y=$\frac{{k}_{2}}{x}$ 在第一象限内的图象依次是C1和C2,设点P在C1上,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,则四边形PAOB的面积为( )| A. | k1+k2 | B. | k1-k2 | C. | k1•k2 | D. | k1•k2-k2 |
4. 如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
 如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )
如图,平行四边形ABCD中,对角线AC与BD相交于点O,且AB⊥AC,AB=3,OC=4,则BD的长为( )| A. | 4 | B. | 5 | C. | 10 | D. | 12 |
1. 如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
 如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
如图,OB是∠AOC的平分线,OD是∠COE的平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
2.把汽油以均匀的速度注入容积为60L的桶里.注入的时间和注入的油量如下表:
(1)求q与t的函数解析式.并判断q是否是t的正比例函数;
(2)求变量t的取值范围;
(3)求t=1.5,4.5时,q的对应值.
| 注入的时间(min) | 1 | 2 | 3 | 4 | 5 | 6 |
| 注入油量q(L) | 1.5 | 3 | 4.5 | 6 | 7.5 | 9 |
(2)求变量t的取值范围;
(3)求t=1.5,4.5时,q的对应值.
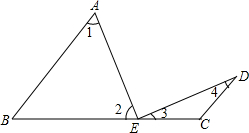 已知:如图,AB∥DC,点E是BC上一点,AB=BE,CD=CE.求证:AE⊥DE.
已知:如图,AB∥DC,点E是BC上一点,AB=BE,CD=CE.求证:AE⊥DE.