题目内容
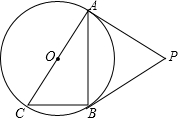 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.(1)求证:PB是⊙O的切线;
(2)已知PA=
| 3 |
考点:切线的判定与性质,线段垂直平分线的性质,解直角三角形
专题:
分析:(1)连结OB,由OA=OB,得∠OAB=∠OBA,再根据PA=PB,得∠PAB=∠PBA,从而得出∠PAO=∠PBO,由PA是⊙O的切线可推得∠PBO=90°,即OB⊥PB,所以PB是⊙O的切线;
(2)连结OP,根据PA=PB,则点P在线段AB的垂直平分线上,再由OA=OB,则点O在线段AB的垂直平分线上,从而得出OP垂直平分线段AB,根据BC⊥AB,得出PO∥BC,则∠AOP=∠ACB=60°,在Rt△APO中,利用tan∠AOP=
,求出AP,即可得出答案.
(2)连结OP,根据PA=PB,则点P在线段AB的垂直平分线上,再由OA=OB,则点O在线段AB的垂直平分线上,从而得出OP垂直平分线段AB,根据BC⊥AB,得出PO∥BC,则∠AOP=∠ACB=60°,在Rt△APO中,利用tan∠AOP=
| AP |
| AO |
解答: 证明:(1)连结OB,
证明:(1)连结OB,
∵OA=OB,
∴∠OAB=∠OBA,
∵PA=PB,
∴∠PAB=∠PBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,即∠PAO=∠PBO,
又∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠PBO=90°,
∴OB⊥PB,
又∵OB是⊙O半径,
∴PB是⊙O的切线;
(2)连结OP,
∵PA=PB,
∴点P在线段AB的垂直平分线上,
∵OA=OB,
∴点O在线段AB的垂直平分线上,
∴OP垂直平分线段AB,
又∵BC⊥AB,
∴PO∥BC,
∴∠AOP=∠ACB=60°,
∵在Rt△APO中,tan∠AOP=
=tan 60°=
,AP=
,
∴AO=1,
∴⊙O的半径为1.
 证明:(1)连结OB,
证明:(1)连结OB,∵OA=OB,
∴∠OAB=∠OBA,
∵PA=PB,
∴∠PAB=∠PBA,
∴∠OAB+∠PAB=∠OBA+∠PBA,即∠PAO=∠PBO,
又∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠PBO=90°,
∴OB⊥PB,
又∵OB是⊙O半径,
∴PB是⊙O的切线;
(2)连结OP,
∵PA=PB,
∴点P在线段AB的垂直平分线上,
∵OA=OB,
∴点O在线段AB的垂直平分线上,
∴OP垂直平分线段AB,
又∵BC⊥AB,
∴PO∥BC,
∴∠AOP=∠ACB=60°,
∵在Rt△APO中,tan∠AOP=
| AP |
| AO |
| 3 |
| 3 |
∴AO=1,
∴⊙O的半径为1.
点评:本题考查了切线的判定和性质、线段的垂直平分线以及解直角三角形的综合运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
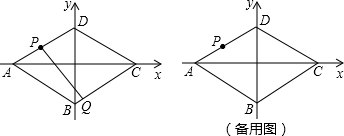
 如图,抛物线y=ax2+bx+c关于直线x=-1对称,与坐标轴交于A、B、C三点,且AB=4,点D的坐标为(-2,-
如图,抛物线y=ax2+bx+c关于直线x=-1对称,与坐标轴交于A、B、C三点,且AB=4,点D的坐标为(-2,-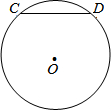 如图,CD是⊙O的弦,且CD=6.根据以上条件你能求出⊙O的半径吗?
如图,CD是⊙O的弦,且CD=6.根据以上条件你能求出⊙O的半径吗?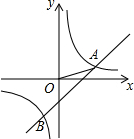 如图,在平面直角坐标系中,O为原点,一次函数y=kx+b与反比例函数
如图,在平面直角坐标系中,O为原点,一次函数y=kx+b与反比例函数