��Ŀ����
 ��ͼ��������y=ax2+bx+c����ֱ��x=-1�Գƣ��������ύ��A��B��C���㣬��AB=4����D������Ϊ��-2��-
��ͼ��������y=ax2+bx+c����ֱ��x=-1�Գƣ��������ύ��A��B��C���㣬��AB=4����D������Ϊ��-2��-| 3 |
| 2 |
��1���������ߵĽ���ʽ��
��2����ֱ��lƽ���ı���OCDA���������k��ֵ��
��3��������������ƽ��1����λ��������ƽ��2����λ��������������ֱ��l����M��N���㣬������M����y����࣬N����y���Ҳࣩ����y��ĸ��������Ƿ����һ����P��ʹ�ò���kȡ��ֵ��ֱ��PM��PN���ǹ���y��Գƣ������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺
��������1�����ݶԳƣ��ɵ�A��B������꣬���ݴ���ϵ�������ɵô𰸣�
��2�����ݽⷽ���飬�ɵý������꣬����ƽ���ı��������ȣ��ɵ�����ƽ���ı��ε����µĺ���ȣ����ݽⷽ�̣��ɵô𰸣�
��3������������ƽ�ƣ��ɵý���ʽΪ��y=
x2������������ȵ��������������ƣ��ɵ�Rt��MPM1��Rt��NPN1���������������ε����ʣ��ɵö�Ӧ�ߵı���ȣ����ݽⷽ�̣��ɵô𰸣�
��2�����ݽⷽ���飬�ɵý������꣬����ƽ���ı��������ȣ��ɵ�����ƽ���ı��ε����µĺ���ȣ����ݽⷽ�̣��ɵô𰸣�
��3������������ƽ�ƣ��ɵý���ʽΪ��y=
| 1 |
| 2 |
����⣺��1��������y=ax2+bx+c����ֱ��x=-1�Գƣ�AB=4��
��A��-3��0��B��1��0��
�֡ߵ�D������Ϊ��-2��-
������������
��
��
���
��
�������ߵĽ���ʽΪ y=
x2+x-
��
��2���ɣ�1����֪ y=
x2+x-
��x=0��C�����꣨0��-
��
��CD��AB
L��AB���ڵ�E����CD���ڵ�F
��E���������
���E��-
��0��
F���������
���F��-
��-
��
����S�ı���OCEF=S�ı���EFDA��
��OE+CF=DF+AE
��|-
|+|-
|=��3-|-
|��+��2-|-
|��
��k��0
��
+
=3-
+2-
���k=
��3�����ڶ���P��ʹ�ò���kȡ��ֵ��ֱ��PM��PN���ǹ���y��Գ�
�ɣ�1 ��֪y=
x2+x-
=
(x2+2x+1-1)-
=
(x+1)2-2
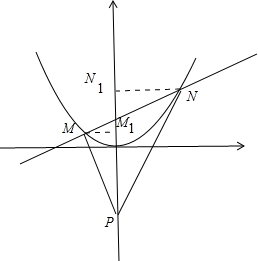
��������ƽ��1����λ��������ƽ��2����λ���������ߵĽ���ʽΪ��y=
x2
��ͼ������y���ϴ���һ��P��0��t�� ��t��0��
ʹֱ��PM��PN����y��Գƣ�����M��N�ֱ���y��������MM1��NN1������ֱ�ΪM1��N1
�ߡ�MPO=��NPO
��Rt��MPM1��Rt��NPN1
��
=
��
���M��xm��ym���ڵ�N��xn��yn�������
��P��y�ĸ�������
���ʽ��Ϊ
=
��
=
�֡�ym=kxm+2 yn=kxn+2
��
=
�����t��xm-xn0=-2��xm-xn��
��xm��xn
��t=-2 ��������
����y��ĸ��������Ƿ����һ����P��0��-2��ʹֱ��PM��PN���ǹ���y��Գƣ�
��A��-3��0��B��1��0��
�֡ߵ�D������Ϊ��-2��-
| 3 |
| 2 |
��
|
���
|
�������ߵĽ���ʽΪ y=
| 1 |
| 2 |
| 3 |
| 2 |
��2���ɣ�1����֪ y=
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
��CD��AB
L��AB���ڵ�E����CD���ڵ�F
��E���������
|
| 2 |
| k |
F���������
|
| 7 |
| 2k |
| 3 |
| 2 |
����S�ı���OCEF=S�ı���EFDA��
��OE+CF=DF+AE
��|-
| 2 |
| k |
| 7 |
| 2k |
| 2 |
| k |
| 7 |
| 2k |
��k��0
��
| 2 |
| k |
| 7 |
| 2k |
| 2 |
| k |
| 7 |
| 2k |
���k=
| 11 |
| 5 |
��3�����ڶ���P��ʹ�ò���kȡ��ֵ��ֱ��PM��PN���ǹ���y��Գ�
�ɣ�1 ��֪y=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |

��������ƽ��1����λ��������ƽ��2����λ���������ߵĽ���ʽΪ��y=
| 1 |
| 2 |
��ͼ������y���ϴ���һ��P��0��t�� ��t��0��
ʹֱ��PM��PN����y��Գƣ�����M��N�ֱ���y��������MM1��NN1������ֱ�ΪM1��N1
�ߡ�MPO=��NPO
��Rt��MPM1��Rt��NPN1
��
| MM1 |
| NN1 |
| PM1 |
| PN1 |
���M��xm��ym���ڵ�N��xn��yn�������
��P��y�ĸ�������
���ʽ��Ϊ
| -xm |
| xn |
| -t+ym |
| -t+yn |
| xm |
| xn |
| t-ym |
| t-yn |
�֡�ym=kxm+2 yn=kxn+2
��
| xm |
| xn |
| t-kxm-2 |
| t-kxn-2 |
�����t��xm-xn0=-2��xm-xn��
��xm��xn
��t=-2 ��������
����y��ĸ��������Ƿ����һ����P��0��-2��ʹֱ��PM��PN���ǹ���y��Գƣ�
���������⿼���˶��κ������ۺ��⣬����ϵ���������ʽ����2�����������������ȵó�����ʽ����ؼ�����3�������������εĶ�Ӧ����ȵó������ǽ���ؼ���

��ϰ��ϵ�д�
�����Ŀ
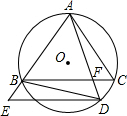 ��ͼ����ABC�ڽ��ڡ�O����D�ڻ�BC�ϣ�����D��DE��BC����ֱ��AB�ڵ�E������AD��BC�ڵ�F������BD������ADB=��E��
��ͼ����ABC�ڽ��ڡ�O����D�ڻ�BC�ϣ�����D��DE��BC����ֱ��AB�ڵ�E������AD��BC�ڵ�F������BD������ADB=��E��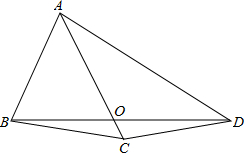 ��ͼ�����ı���ABCD�У��߶�AC��BD�ཻ��O��AB=BC=CD����ABC=70�㣬��BCD=170�㣬���BAD�Ķ�����
��ͼ�����ı���ABCD�У��߶�AC��BD�ཻ��O��AB=BC=CD����ABC=70�㣬��BCD=170�㣬���BAD�Ķ�����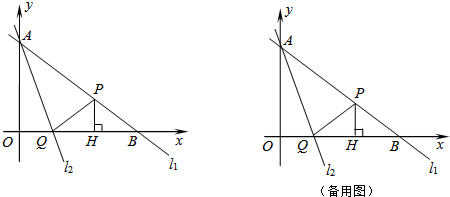
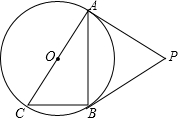 ��ͼ����O��Rt��ABC�����Բ����ABC=90�㣬��P��Բ��һ�㣬PA�С�O�ڵ�A����PA=PB��
��ͼ����O��Rt��ABC�����Բ����ABC=90�㣬��P��Բ��һ�㣬PA�С�O�ڵ�A����PA=PB��