题目内容
在-2,-3,4这三个数中抽取2个数分别作为点P的横坐标和纵坐标.
(1)求P点的横纵坐标之积为负数的概率;
(2)求过点P的所有正比例函数中,出现函数y随自变量x的增大而增大的概率为多少?
(1)求P点的横纵坐标之积为负数的概率;
(2)求过点P的所有正比例函数中,出现函数y随自变量x的增大而增大的概率为多少?
考点:列表法与树状图法,正比例函数的性质
专题:
分析:(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与P点的横纵坐标之积为负数的情况,再利用概率公式即可求得答案;
(2)首先根据题意(1)可知过点P的正比例函数共有6种情况,函数y随自变量x的增大而增大的有2种情况,然后直接利用概率公式求解即可求得答案.
(2)首先根据题意(1)可知过点P的正比例函数共有6种情况,函数y随自变量x的增大而增大的有2种情况,然后直接利用概率公式求解即可求得答案.
解答:解:(1)画树状图得:
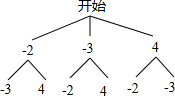
∵共有6种等可能的结果,P点的横纵坐标之积为负数的有4种情况,
∴P点的横纵坐标之积为负数的概率为:
=
;
(2)∵过点P的正比例函数共有6种情况,函数y随自变量x的增大而增大的有2种情况,
∴出现函数y随自变量x的增大而增大的概率为:
=
.

∵共有6种等可能的结果,P点的横纵坐标之积为负数的有4种情况,
∴P点的横纵坐标之积为负数的概率为:
| 4 |
| 6 |
| 2 |
| 3 |
(2)∵过点P的正比例函数共有6种情况,函数y随自变量x的增大而增大的有2种情况,
∴出现函数y随自变量x的增大而增大的概率为:
| 2 |
| 6 |
| 1 |
| 3 |
点评:本题考查的是用列表法或画树状图法求概率以及正比例函数的性质.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目

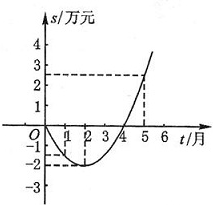 下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:
下面的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题: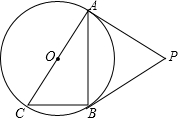 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB. 如图,AB∥CD,∠1=∠2,∠BEF与∠EFC相等吗?为什么?
如图,AB∥CD,∠1=∠2,∠BEF与∠EFC相等吗?为什么? 如图,在菱形ABCD中,∠ABC=60°,BC=1cm,以DC为边在菱形的外部作正三角形CDE,连接AE,则AE=
如图,在菱形ABCD中,∠ABC=60°,BC=1cm,以DC为边在菱形的外部作正三角形CDE,连接AE,则AE=