题目内容
8.观察下列的变形及规律:$\frac{1}{1×2}$=1-$\frac{1}{2}$;$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$;$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$;…
(1)若n为正整数,请你猜想$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)证明你的结论;
(3)利用上述规律计算:$\frac{1}{n(n+2)}$+$\frac{1}{(n+2)(n+4)}$+$\frac{1}{(n+4)(n+6)}$.
分析 (1)根据已知数据分母的变化直接猜想得出即可;
(2)利用分式的加减运算法则化简得出即可;
(3)利用拆项法变形可得$\frac{1}{n(n+2)}$=$\frac{1}{2}×$($\frac{1}{n}$-$\frac{1}{n+2}$),进而可得$\frac{1}{(n+2)(n+4)}$=$\frac{1}{2}$($\frac{1}{n+2}$-$\frac{1}{n+4}$),$\frac{1}{(n+4)(n+6)}$=$\frac{1}{2}$($\frac{1}{n+4}$-$\frac{1}{n+6}$),然后再计算即可.
解答 (1)解:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)证明:右边=$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{n+1}{n(n+1)}$-$\frac{n}{n(n+1)}$=$\frac{n+1-n}{n(n+1)}$=$\frac{1}{n(n+1)}$=左边,
所以猜想成立.
(3)原式=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$+$\frac{1}{n+2}$-$\frac{1}{n+4}$+$\frac{1}{n+4}$-$\frac{1}{n+6}$),
=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+6}$),
=$\frac{1}{2}$•$\frac{n+6-n}{n(n+6)}$,
=$\frac{1}{2}$×$\frac{6}{n(n+6)}$,
=$\frac{3}{n(n+6)}$.
点评 此题主要考查了分式的加减计算,关键是利用拆项法找出计算规律.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
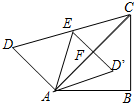 如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )
如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB=$6\sqrt{2}$cm,点D′到BC的距离是( )| A. | $3+\sqrt{3}$ | B. | $3\sqrt{2}+\sqrt{6}$ | C. | $3\sqrt{2}-\sqrt{6}$ | D. | $3-\sqrt{3}$ |
| A. | x=-1 | B. | x=1 | C. | x=-$\frac{1}{2}$ | D. | x=±1 |
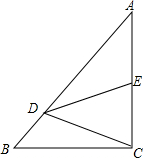 如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值.
如图,在Rt△ABC中,∠ACB=90°,点D在边AB上,线段DC绕点D按逆时针旋转,端点C恰巧落在边AC上的点E处,已知$\frac{AD}{DB}$=4,求$\frac{AE}{EC}$的值. 如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则sin∠BAG=$\frac{\sqrt{10}}{10}$.
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长交BC于点G,连接AG.则sin∠BAG=$\frac{\sqrt{10}}{10}$.