题目内容
1.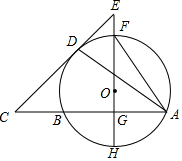 已知,FH是⊙O的直径,弦AB⊥FH于G,过AB的延长线上一点C作⊙O的切线交HF于E,切点为点D,连接AF、AD.
已知,FH是⊙O的直径,弦AB⊥FH于G,过AB的延长线上一点C作⊙O的切线交HF于E,切点为点D,连接AF、AD.(1)求证:∠DAF=$\frac{1}{2}$∠C;
(2)若AB=6,GH=$\frac{3}{2}$,求AF的长.
分析 (1)连接OD,如图,先利用切线的性质得∠ODC=90°,则根据四边形的内角和得到∠C+∠DOG=180°,再利用等角的补角相等得到∠DOF=∠C,然后根据圆周角定理可得到结论;
(2)连接OA,如图,设⊙O的半径为r,利用垂径定理得到AG=BG=$\frac{1}{2}$AB=3,再根据勾股定理得到在(r-$\frac{3}{2}$)2+32=r2,解得r=$\frac{15}{4}$,所以FG=FH-OG=6,然后在Rt△AFG中利用勾股定理可计算出AF.
解答 (1)证明:连接OD,如图,
∵CD为切线,
∴OD⊥CD,
∴∠ODC=90°,
∵OG⊥AB,
∴∠OGC=90°,
∴∠C+∠DOG=180°,
而∠DOF+∠DOG=180°,
∴∠DOF=∠C,
∵∠DAF=$\frac{1}{2}$∠DOF,
∴∠DAF=$\frac{1}{2}$∠C;
(2)解:连接OA,如图,设⊙O的半径为r,
∵OG⊥AB,
∴AG=BG=$\frac{1}{2}$AB=3,
在Rt△OGA中,OG=r-$\frac{3}{2}$,OA=r,
∴(r-$\frac{3}{2}$)2+32=r2,解得r=$\frac{15}{4}$,
∴FG=FH-OG=$\frac{15}{4}$×2-$\frac{3}{2}$=6,
在Rt△AFG中,AF=$\sqrt{{3}^{2}+{6}^{2}}$=3$\sqrt{5}$.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了垂径定理和圆周角定理.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
12.一个弹簧原长(不挂重物)15cm,弹簧总长L(cm)与所挂物体的质量x(千克)的关系如下表所示:
(1)求L与x之间的关系式;
(2)重物为5(千克)时弹簧总长L(cm)是多少?
| 弹簧总长L/cm | 16 | 17 | 18 | 19 | 20 |
| 重物质量x/千克 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
(2)重物为5(千克)时弹簧总长L(cm)是多少?
9.下列说法错误的是( )
| A. | 一组对边平行且另一组对边相等的四边形是平行四边形 | |
| B. | 两组对角都相等的四边形是平行四边形 | |
| C. | 一组对边平行且一组对角相等的四边形是平行四边形 | |
| D. | 一组对边平行,一组邻角互补的四边形是平行四边形 |
16.已知x-y=-3,xy=2,则(x+2)(y-2)的值是( )
| A. | 4 | B. | -8 | C. | 12 | D. | 0 |
10. 如图,将一副三角板如图放置,若AE∥BC,则∠FAD=( )
如图,将一副三角板如图放置,若AE∥BC,则∠FAD=( )
 如图,将一副三角板如图放置,若AE∥BC,则∠FAD=( )
如图,将一副三角板如图放置,若AE∥BC,则∠FAD=( )| A. | 25° | B. | 20° | C. | 15° | D. | 10° |
 如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C.
如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(-4,0)、B(0,3),抛物线y=-x2+2x+1与y轴交于点C. 如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点.
如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点. 如图,△AOB中,点C为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过A,C两点,若△AOB的面积为12,则k的值是( )
如图,△AOB中,点C为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过A,C两点,若△AOB的面积为12,则k的值是( )