题目内容
8.甲列车速度是60km/h,乙列车速度是90km/h.(1)两列车都从某地出发,目的地距离出发点1000km,甲列车先走2小时,问乙列车什么时候能追上甲列车?追上时离目的地还有多远?
(2)甲列车从A地开往B地,乙列车同时从B地开往A地,已知A,B两地相距200km,两车相遇的地方离A地多远?(用方程)
分析 (1)设乙列车经过x小时追上甲列车,根据两列车行驶的路程差为60×2=120km列出方程解答即可;进一步根据乙列车行的路程求得追上时离目的地还有多远即可;
(2)设两车相遇时间为y小时,根据所行的路程和为200km列出方程求得相遇时间,进一步求得两车相遇的地方离A地多远即可.
解答 解:(1)设乙列车经过x小时追上甲列车,由题意得
90x-60x=60×2,
解得:x=4,
则1000-90×4=640km.
答:乙列车经过4小时能追上甲列车,追上时离目的地还有640km.
(2)设两车相遇时间为y小时,由题意得
90y+60y=200,
解得:y=$\frac{4}{3}$,
60y=80.
答:两车相遇的地方离A地80km.
点评 此题考查一元一次方程的实际运用,掌握行程问题中的基本数量关系是解决问题的关键.

练习册系列答案
相关题目
18.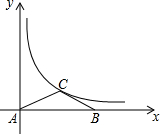 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
 如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )
如图,等腰三角形ABC的顶点A在原点,顶点B在x轴的正半轴上,顶点C在函数y=$\frac{k}{x}$(x>0)的图象上运动,且AC=BC,则△ABC的面积大小变化情况是( )| A. | 一直不变 | B. | 先增大后减小 | C. | 先减小后增大 | D. | 先增大后不变 |