题目内容
10．古希腊科学家海伦发现：“如果△ABC三边长分别为a、b、c，记p=$\frac{a+b+c}{2}$，那么△ABC的面积为S=$\sqrt{p（p-a）（p-b）（p-c）}$”．若已知△ABC的三边长a=5、b=7、c=8，则该三角形的面积为（ ）| A． | $\frac{35}{2}$ | B． | 10 | C． | 8$\sqrt{2}$ | D． | 10$\sqrt{3}$ |
分析 直接求出p的值，进而利用S=$\sqrt{p（p-a）（p-b）（p-c）}$求出答案．
解答 解：由题意知，p=$\frac{a+b+c}{2}$=$\frac{5+7+8}{2}$=10，
所以S=$\sqrt{p（p-a）（p-b）（p-c）}$=$\sqrt{10×（10-5）（10-7）（10-8）}$=10$\sqrt{3}$．
故选：D．
点评 此题主要考查了二次根式的应用，正确得出p的值是解题关键．
练习册系列答案
相关题目
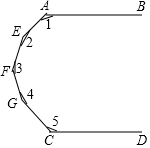如图，AB∥CD，则∠1+∠2+∠3+∠4+∠5=720°．
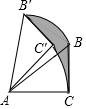如图，在△ABC中，∠ACB=90°，BC=5，将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置，则线段BC扫过的区域（图中阴影部分）面积为$\frac{25π}{8}$．
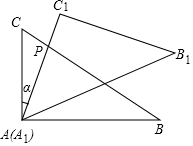如图，是一副三角板，在△ABC 中，∠A=90°，∠C=60°，∠B=30°；在△A1B1C1中，∠C1=90°，∠A1=45°，∠B1=45°，且A1B1=AB．若将边A1C1与边AC重合，其中点A1与点A重合．将三角板A1B1C1绕点A（A1）按顺时针方向旋转，旋转角为α，旋转过程中边A1C1与边BC的交点为P，设AC=m．