题目内容
5.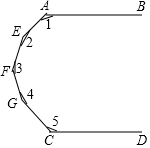 如图,AB∥CD,则∠1+∠2+∠3+∠4+∠5=720°.
如图,AB∥CD,则∠1+∠2+∠3+∠4+∠5=720°.
分析 过∠2、∠3…的顶点作a的平行线,然后根据两直线平行,同旁内角互补解答.
解答 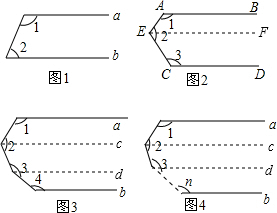 解:如图1,∵a∥b,
解:如图1,∵a∥b,
∴∠1+∠2=180°;
如图2,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠AEF=180°,
∠CEF+∠2=180°,
∴∠1+∠AEF+∠CEF+∠2=180°+180°,
即∠1+∠2+∠3=360°;
如图3,过∠2、∠3的顶点作a的平行线,
则∠1+∠2+∠3+∠4=180°×3=540°;
如图4,过∠2、∠3…的顶点作a的平行线,
则∠1+∠2+∠3+∠4+…+∠n=(n-1)•180°.
∴∠1+∠2+∠3+∠4+∠5=(5-1)•180°=720°,
故答案为:720°.
点评 本题主要考查了两直线平行,同旁内角互补的性质,过拐点作平行线是解题的关键,也是本题的难点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.以下问题,不适合使用全面调查的是( )
| A. | 对旅客上飞机前的安检 | |
| B. | 航天飞机升空前的安全检查 | |
| C. | 了解全班学生的体重 | |
| D. | 了解广州市中学生每周使用手机所用的时间 |
20.若一个数的立方根和算术平方根都等于它本身,则这个数一定是( )
| A. | 0或1 | B. | 1或-1 | C. | 0或±1 | D. | 0 |
10.古希腊科学家海伦发现:“如果△ABC三边长分别为a、b、c,记p=$\frac{a+b+c}{2}$,那么△ABC的面积为S=$\sqrt{p(p-a)(p-b)(p-c)}$”.若已知△ABC的三边长a=5、b=7、c=8,则该三角形的面积为( )
| A. | $\frac{35}{2}$ | B. | 10 | C. | 8$\sqrt{2}$ | D. | 10$\sqrt{3}$ |
 如图,已知△ABC,按要求画图、填空:
如图,已知△ABC,按要求画图、填空: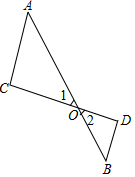 如图,AB与CD相交于点O,∠A=∠1,∠B=∠2.求证:AC∥DB.
如图,AB与CD相交于点O,∠A=∠1,∠B=∠2.求证:AC∥DB.