题目内容
2.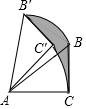 如图,在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,则线段BC扫过的区域(图中阴影部分)面积为$\frac{25π}{8}$.
如图,在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,则线段BC扫过的区域(图中阴影部分)面积为$\frac{25π}{8}$.
分析 根据题意和图形可以得到阴影部分的面积是扇形ABB′的面积与△ABC的面积之和减去△AB′C′的面积再减去扇形ACC′的面积,从而可以解答本题.
解答 解:∵在△ABC中,∠ACB=90°,BC=5,将△ABC绕顶点A按逆时针方向旋转45°至△AB′C′的位置,
∴△ABC≌△AB′C′,
∴线段BC扫过的区域(图中阴影部分)面积为:S扇形ABB′+S△ABC-S△AB′C′-S扇形ACC′=S扇形ABB′-S扇形ACC′=$\frac{45×π×A{B}^{2}}{360}-\frac{45×π×A{C}^{2}}{360}$=$\frac{π(A{B}^{2}-A{C}^{2})}{8}=\frac{π•B{C}^{2}}{8}=\frac{25π}{8}$,
故答案为:$\frac{25π}{8}$.
点评 本题考查扇形面积的计算、旋转的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
相关题目
10.古希腊科学家海伦发现:“如果△ABC三边长分别为a、b、c,记p=$\frac{a+b+c}{2}$,那么△ABC的面积为S=$\sqrt{p(p-a)(p-b)(p-c)}$”.若已知△ABC的三边长a=5、b=7、c=8,则该三角形的面积为( )
| A. | $\frac{35}{2}$ | B. | 10 | C. | 8$\sqrt{2}$ | D. | 10$\sqrt{3}$ |
7.下列图中不是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
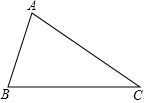 如图,已知△ABC,按要求画图、填空:
如图,已知△ABC,按要求画图、填空: 画出下列几何体的三视图.
画出下列几何体的三视图.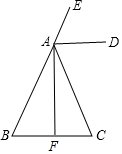 如图,已知∠EAC是△ABC的外角,AD平分∠EAC,AD∥BC,点F为BC中点.
如图,已知∠EAC是△ABC的外角,AD平分∠EAC,AD∥BC,点F为BC中点.