题目内容
18.计算:3$\sqrt{12}$×$\frac{\sqrt{2}}{2}$÷$\sqrt{24}$+($\sqrt{3}$+2)2(4$\sqrt{3}$-7).分析 先根据二次根式的乘除法则和完全平方公式运算,然后利用平方差公式.
解答 解:原式=$\frac{3}{2}$$\sqrt{12×\frac{1}{2}×\frac{1}{24}}$+(4$\sqrt{3}$+7)(4$\sqrt{3}$-7)
=$\frac{3}{2}$×$\frac{1}{2}$+48-49
=-$\frac{1}{4}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
9.将一元一次方程$\frac{x}{3}$-5=$\frac{x-1}{2}$去分母后,正确的是( )
| A. | x-5=x-1 | B. | 2x-5=3x-1 | C. | 2x-30=3x-3 | D. | 2x-30=3x-1 |
10.古希腊科学家海伦发现:“如果△ABC三边长分别为a、b、c,记p=$\frac{a+b+c}{2}$,那么△ABC的面积为S=$\sqrt{p(p-a)(p-b)(p-c)}$”.若已知△ABC的三边长a=5、b=7、c=8,则该三角形的面积为( )
| A. | $\frac{35}{2}$ | B. | 10 | C. | 8$\sqrt{2}$ | D. | 10$\sqrt{3}$ |
7.下列图中不是正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
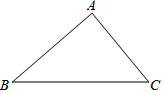 已知,如图,在△ABC中,∠B=45°,∠C=60°,AB=3$\sqrt{2}$.
已知,如图,在△ABC中,∠B=45°,∠C=60°,AB=3$\sqrt{2}$.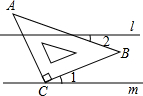 如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的和是多少度?并证明你的结论.
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的和是多少度?并证明你的结论.