题目内容
3.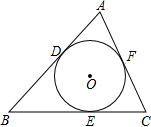 如图,⊙O是△ABC的内切圆,点D、E、F为切点,AD=13,AC=25,BC=35,求BD的长度.
如图,⊙O是△ABC的内切圆,点D、E、F为切点,AD=13,AC=25,BC=35,求BD的长度.
分析 设BD=xcm,由于⊙O是△ABC的内切圆,则根据切线长定理得到AD=AF=13,BD=BE=x,CE=CF,然后利用CE=BC-BE=35-x,CF=AC-AF=12得到35-x=12,再解方程求出x即可.
解答 解:设BD=xcm,
∵⊙O是△ABC的内切圆,点D、E、F为切点,
∴AD=AF=13,BD=BE=x,CE=CF,
而CE=BC-BE=35-x,CF=AC-AF=25-13=12,
∴35-x=12,
解得x=23,
即BD的长为23cm.
点评 本题考查了三角形的内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.三角形的内心就是三角形三个内角角平分线的交点.也考查了切线长定理.

练习册系列答案
相关题目
15.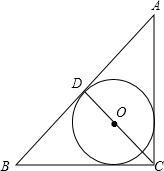 在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
 在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )
在Rt△ABC中,CD是斜边AB上的高,则图中的三个直角三角形(△ABC、△ACD、△BCD)的内切圆半径的和等于( )| A. | CD | B. | BC | C. | AC | D. | AB |
 如图,在△ABC中,若D、E分别是AB、AC上的点,且DE∥BC,AD=1,BD=2,则DE:BC=1:3.
如图,在△ABC中,若D、E分别是AB、AC上的点,且DE∥BC,AD=1,BD=2,则DE:BC=1:3. 如图,已知线段AC,BD相交于点O,且OA=OC,OB=OD,E,F分别为DO,BO上两点,DE=BF,CE=9,求AF的长.
如图,已知线段AC,BD相交于点O,且OA=OC,OB=OD,E,F分别为DO,BO上两点,DE=BF,CE=9,求AF的长.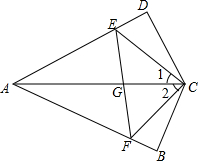 如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.
如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.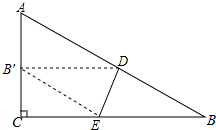 如图是一张直角三角形纸片,∠C=90°,点D在边AB上,若将三角形纸片沿直线DE折叠,使点B落在AC边上,记作点B′,连接B′E.
如图是一张直角三角形纸片,∠C=90°,点D在边AB上,若将三角形纸片沿直线DE折叠,使点B落在AC边上,记作点B′,连接B′E.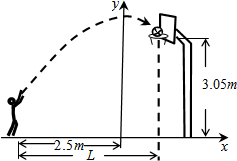 李老师在某次投篮中,球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分,其相关数据如图所示,若命中篮圈中心,则他与蓝底的距离L为4米;若身高为1.79米的李老师是跳投命中篮圈中心的,且篮球在离李老师的头顶上方0.25米处出手,那么跳投时他跳离地面的高度为0.21米.
李老师在某次投篮中,球的运动路线是抛物线$y=-\frac{1}{5}{x^2}+3.5$的一部分,其相关数据如图所示,若命中篮圈中心,则他与蓝底的距离L为4米;若身高为1.79米的李老师是跳投命中篮圈中心的,且篮球在离李老师的头顶上方0.25米处出手,那么跳投时他跳离地面的高度为0.21米.