题目内容
11.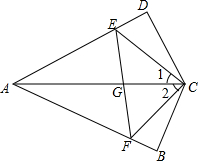 如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.
如图所示,∠1=∠2,CD⊥AD,CB⊥AB.CD=CB,AC、EF相交于点G.求证:AC垂直平分EF.
分析 由CD⊥AD,CB⊥AB,CD=CB,可知AC是B的线,根据ASA可证△AEC≌△AFC,得到AE=AF,根据等腰三角形的性质可知AC垂直平分EF.
解答 证明:∵CD⊥AD,CB⊥AB,CD=CB,
∴∠EAC=∠FAC,
在△AEC和△AFC中,
$\left\{\begin{array}{l}{∠EAC=∠FAC}\\{AC=AC}\\{∠1=∠2}\end{array}\right.$,
∴△AEC≌△AFC(ASA),
∴AE=AF,
∴AC垂直平分EF(三线合一).
点评 本题主要考查了全等三角形的判定与性质、角平分线的判定以及等腰三角形的性质,证明△AEC≌△AFC是解决问题的关键.

练习册系列答案
相关题目
7.已知扇形的弧长为20cm,面积为100cm2,则该扇形的半径为( )
| A. | 5πcm | B. | 5cm | C. | 10πcm | D. | 10cm |
 已知:如图,点A、B、C、D在同一条直线上,AC=DB,∠ABE=∠DCF,BE=CF,求证:AE∥DF.
已知:如图,点A、B、C、D在同一条直线上,AC=DB,∠ABE=∠DCF,BE=CF,求证:AE∥DF.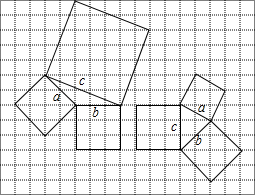
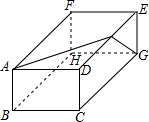 如图是一个长方体,AB=3,BC=5,AF=6.要在长方体上系一根绳子连接A、G,则绳子至少要多长?(接头处长度不计)
如图是一个长方体,AB=3,BC=5,AF=6.要在长方体上系一根绳子连接A、G,则绳子至少要多长?(接头处长度不计)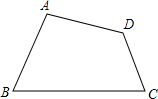 如图:四边形ABCD中,∠D=120°,∠C=75°,AD=4,CD=2$\sqrt{3}$-2,cosB=$\frac{3}{5}$,求BC的长.
如图:四边形ABCD中,∠D=120°,∠C=75°,AD=4,CD=2$\sqrt{3}$-2,cosB=$\frac{3}{5}$,求BC的长.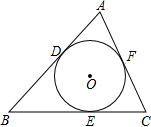 如图,⊙O是△ABC的内切圆,点D、E、F为切点,AD=13,AC=25,BC=35,求BD的长度.
如图,⊙O是△ABC的内切圆,点D、E、F为切点,AD=13,AC=25,BC=35,求BD的长度. 如图所示,把直角三角形ABC折叠,使A与B点重合,得到折痕DE,折叠点C恰好与D点重合,求∠ABC,∠BDE的度数.
如图所示,把直角三角形ABC折叠,使A与B点重合,得到折痕DE,折叠点C恰好与D点重合,求∠ABC,∠BDE的度数.