Question

5．如图，点A（0，a），B（b，0）分别在y轴正半轴、x轴正半轴上，C为AB的中点，a，b满足a²-2ab+b²=-|b-4|．
（1）写出A，B两点坐标，并判断△AOB的形状；
（2）若一直角三角板直角顶点与C重合，两边分别交OA，OB交于E，F两点，求OE+OF的值．

Answer 1

分析 （1）把a²-2ab+b²=-|b-4|化为（a-b）²+|b-4|=0，得到a=b=4，从而得出A，B两点坐标，也得到OA=OB=4，即可证得结论；
（2）作MC⊥y轴于M，作NC⊥x轴于N，C为AB的中点，可得MC=CN，在证得△MCE≌△NCF，于是证出ME=NF，于是有OE+OF=OM-ME+ON+NF=OM+ON=2+2=4．

解答 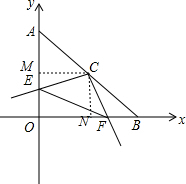解：（1）∵a²-2ab+b²=-|b-4|，
∴（a-b）²+|b-4|=0，
∴a=b=4，
∴A，B两点坐标A（0，4），B（4，），
∴OA=OB=4，
∵AO⊥BO，
∴△AOB是等腰直角三角形；

（2）作MC⊥y轴于M，作NC⊥x轴于N，如图所示：
∵C为AB的中点，
则MC=CN=$\frac{1}{2}BC$=2，四边形OMCN是正方形，∠EMC=∠CNF=90°，
∴OM=ON=MC=CN=2，∠MCN=90°，
∵∠ECF=90°，
∴∠MCE=∠FCN，
在△MCE和△NCF中，
$\left\{\begin{array}{l}{∠MCE=∠FCN}\\{∠CME=∠CNF}\\{CM=CN}\end{array}\right.$，
∴△MCE≌△NCF，
∴ME=NF，
∴OE+OF=OM-ME+ON+NF=OM+ON=2+2=4．

点评 本题考查了非负数的性质，等腰三角形的判定，坐标与图形性质，全等三角形的判定与性质，正方形的判定与性质；通过作辅助线得出正方形和三角形全等是解决问题的关键．