Question

如图，在⊙O中，已知弦AB、CD互相垂直，连接AD、BC，作AD的弦心距OE，求证：CB=2EO．

Answer 1

考点：圆心角、弧、弦的关系,三角形中位线定理,圆周角定理

专题：证明题

分析：连接AO并延长交圆于F，连接DF，CF，BF．先由垂径定理得出E是AD的中点，那么OE是△ADF的中位线，根据三角形中位线定理得到DF=2OE，再由圆周角定理证明BF⊥AB，根据垂直于同一直线的两直线平行得出BF∥CD，由圆心角、弧、弦的关系得到BC=DF，等量代换得出BC=2OE．

解答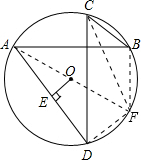：证明：连接AO并延长交圆于F，连接DF，CF，BF．  
∵OE是AD的弦心距，
∴E是AD的中点，
又0是圆心，
∴O是直径AF的中点，
∴OE是△ADF的中位线，
∴DF=2OE．
∵AF是直径，
∴△ABF是直角三角形，且BF⊥AB，
又∵AB⊥CD，
∴BF∥CD，
∴∠FCD=∠BFC，
∴弧DF=弧BC（同圆内相等圆周角所对的圆弧相等），
∴BC=DF（同圆内等弧对等弦），
即BC=2OE．

点评：本题考查了垂径定理，三角形中位线定理，圆周角定理，平行线的判定，圆心角、弧、弦的关系，难度中等．准确作出辅助线得到DF=2OE是解题的关键．