题目内容
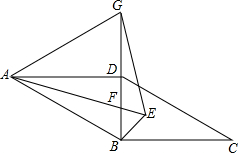 在?ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.
在?ABCD中,对角线BD⊥BC,G为BD延长线上一点且△ABG为等边三角形,∠BAD、∠CBD的平分线相交于点E,连接AE交BD于F,连接GE.(1)若?ABCD的面积为9
| 3 |
(2)求证:AE=BE+GE.
考点:平行四边形的性质,全等三角形的判定与性质
专题:计算题
分析:(1)由三角形ABG为等边三角形,得到三边相等,三角相等且为60°,根据ABCD为平行四边形,得到AD与BC平行,再由BD垂直于BC,得到两个内错角都为90°,进而求出∠DAB=30°,在直角三角形ADB中,利用30°所对的直角边等于斜边的一半表示出BD,进而表示出AD,表示出平行四边形的面积,将表示出的AD,BD,以及已知面积代入求出AG的长;
(2)在AE上取一点Q,使EQ=BE,连接BQ,由AE,BE平分∠BAD、∠DBC,求出∠BAE与∠DBE的度数,利用内角和定理求出∠AEB=60°,由EQ=BE,得到三角形BQE为等边三角形,得到BE=BQ,∠QBE=60°,得到夹角相等,利用SAS得到三角形ABQ与三角形GBE全等,利用全等三角形对应边相等得到AQ=GE,等量代换即可得证.
(2)在AE上取一点Q,使EQ=BE,连接BQ,由AE,BE平分∠BAD、∠DBC,求出∠BAE与∠DBE的度数,利用内角和定理求出∠AEB=60°,由EQ=BE,得到三角形BQE为等边三角形,得到BE=BQ,∠QBE=60°,得到夹角相等,利用SAS得到三角形ABQ与三角形GBE全等,利用全等三角形对应边相等得到AQ=GE,等量代换即可得证.
解答: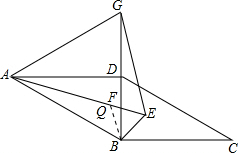 (1)解:∵△ABG为等边三角形,
(1)解:∵△ABG为等边三角形,
∴AB=AG=BG,∠ABG=∠GAB=∠AGB=60°,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵BD⊥BC,
∴∠ADB=∠DBC=90°,
∴∠DAB=
∠GAB=30°,
在Rt△ADB中,BD=
AB,AD=
AB,
∵S平行四边形ABCD=AD•BD=
AB2=9
,
∴AB=6,即AG=6;
(2)证明:在AE上取一点Q,使EQ=BE,连接BQ,
∵AE、BE分别平分∠BAD、∠DBC,
∴∠BAE=
∠BAD=15°,∠DBE=
∠DBC=45°,
∴∠ABE+∠BAE+∠AEB=180°,
∴∠AEB=60°,
∵EQ=BE,
∴△BQE为等边三角形,
∴BE=BQ,∠QBE=60°,
∴∠ABD=∠QBE=60°,
∴∠ABQ=∠FBE,
在△ABQ和△GBE中,
,
∴△ABQ≌△GBE(SAS),
∴AQ=GE,
则AE=AQ+QE=GE+BE.
 (1)解:∵△ABG为等边三角形,
(1)解:∵△ABG为等边三角形,∴AB=AG=BG,∠ABG=∠GAB=∠AGB=60°,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∵BD⊥BC,
∴∠ADB=∠DBC=90°,
∴∠DAB=
| 1 |
| 2 |
在Rt△ADB中,BD=
| 1 |
| 2 |
| ||
| 2 |
∵S平行四边形ABCD=AD•BD=
| ||
| 4 |
| 3 |
∴AB=6,即AG=6;
(2)证明:在AE上取一点Q,使EQ=BE,连接BQ,
∵AE、BE分别平分∠BAD、∠DBC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABE+∠BAE+∠AEB=180°,
∴∠AEB=60°,
∵EQ=BE,
∴△BQE为等边三角形,
∴BE=BQ,∠QBE=60°,
∴∠ABD=∠QBE=60°,
∴∠ABQ=∠FBE,
在△ABQ和△GBE中,
|
∴△ABQ≌△GBE(SAS),
∴AQ=GE,
则AE=AQ+QE=GE+BE.
点评:此题考查了平行四边形的性质,熟练掌握平行四边形的性质是解本题的关键.

练习册系列答案
相关题目
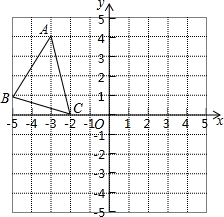 已知直角坐标系中的每个小方格的边长都是1个长度单位,△ABC的位置如图所示,现将△ABC向右平移5个单位,得到△A1B1C1,再向下平移4个单位,得到△A2B2C2.
已知直角坐标系中的每个小方格的边长都是1个长度单位,△ABC的位置如图所示,现将△ABC向右平移5个单位,得到△A1B1C1,再向下平移4个单位,得到△A2B2C2.