题目内容
在同一坐标系中,一次函数y=ax+b与二次函数y=ax2+b的大致图象是( )
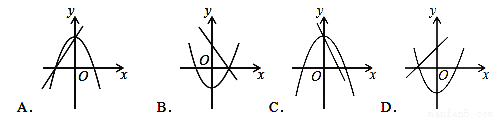
A. A B. B C. C D. D
 C
【解析】解:A.由一次函数y=ax+b的图象可得:a>0,此时二次函数y=ax2+b的图象应该开口向上,故A错误;
B.由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故B错误;
C.由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故C正确;...
C
【解析】解:A.由一次函数y=ax+b的图象可得:a>0,此时二次函数y=ax2+b的图象应该开口向上,故A错误;
B.由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故B错误;
C.由一次函数y=ax+b的图象可得:a<0,b>0,此时二次函数y=ax2+b的图象应该开口向下,顶点的纵坐标大于零,故C正确;...
 名校课堂系列答案
名校课堂系列答案如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张正方形纸片的面积为S3,则这个平行四边形的面积一定可以表示为( )
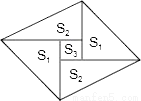
A. 4S1 B. 4S2 C. 4S2+S3 D. 3S1+4S3
 A
【解析】试题分析:设等腰直角三角形的直角边长为a,中间小正方形的边长为b,则另两个直角三角形的边长分别为a-b,a+b,所以S1=,S2=,S3=,平行四边形的面积=2S1+2S2+S3=++=2=4S1,故答案选A.
A
【解析】试题分析:设等腰直角三角形的直角边长为a,中间小正方形的边长为b,则另两个直角三角形的边长分别为a-b,a+b,所以S1=,S2=,S3=,平行四边形的面积=2S1+2S2+S3=++=2=4S1,故答案选A. 如图,在平行四边形ABCD中,∠BAD的平分线AE交BC于点E,且BE=3.若平行四边形ABCD的周长是16,则EC的长为________.

 2
【解析】试题分析:由平行四边形的性质和已知条件证出∠BAE=∠BEA,证出AB=BE=3;求出AB+BC=8,得出BC=5,即可得出EC的长.∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,AD=BC,∴∠AEB=∠DAE,
∵平行四边形ABCD的周长是16,∴AB+BC=8,∵AE是∠BAD的平分线,∴∠BAE=∠DAE,
∴∠BAE=∠AEB,∴AB=BE=3,∴...
2
【解析】试题分析:由平行四边形的性质和已知条件证出∠BAE=∠BEA,证出AB=BE=3;求出AB+BC=8,得出BC=5,即可得出EC的长.∵四边形ABCD是平行四边形,∴AD∥BC,AB=CD,AD=BC,∴∠AEB=∠DAE,
∵平行四边形ABCD的周长是16,∴AB+BC=8,∵AE是∠BAD的平分线,∴∠BAE=∠DAE,
∴∠BAE=∠AEB,∴AB=BE=3,∴... 如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
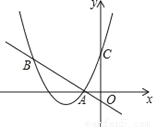
 (1)抛物线解析式为y=x2+4x+3,一次函数解析式为y=﹣x﹣1;(2)由图象可知,满足(x+2)2+m≥kx+b的x的取值范围为x?﹣4或x≥﹣1.
【解析】(1)先利用待定系数法先求出m,再求出点B坐标,利用方程组求出太阳还是解析式.
(2)根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围.
【解析】
(1)∵抛物线y=(x+2)2+m经过点A(﹣1,0...
(1)抛物线解析式为y=x2+4x+3,一次函数解析式为y=﹣x﹣1;(2)由图象可知,满足(x+2)2+m≥kx+b的x的取值范围为x?﹣4或x≥﹣1.
【解析】(1)先利用待定系数法先求出m,再求出点B坐标,利用方程组求出太阳还是解析式.
(2)根据二次函数的图象在一次函数的图象上面即可写出自变量x的取值范围.
【解析】
(1)∵抛物线y=(x+2)2+m经过点A(﹣1,0... 二次函数y=ax2+bx+c的图象如图11所示,且P=|2a+b|+|3b-2c|,Q=|2a-b|-|3b+2c|,则P,Q的大小关系是______.
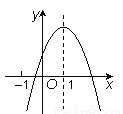
 P>Q
【解析】∵抛物线的开口向下,
∴a<0,
∵
∴b>0,
∴2a-b<0,
∵
∴b+2a=0,
x=-1时,y=a-b+c<0.
∴
∴3b-2c>0,
∵抛物线与y轴的正半轴相交,
∴c>0,
∴3b+2c>0,
∴P=3b-2c,
Q=b-2a-3b-2c=-2a-2b-2c,
∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-...
P>Q
【解析】∵抛物线的开口向下,
∴a<0,
∵
∴b>0,
∴2a-b<0,
∵
∴b+2a=0,
x=-1时,y=a-b+c<0.
∴
∴3b-2c>0,
∵抛物线与y轴的正半轴相交,
∴c>0,
∴3b+2c>0,
∴P=3b-2c,
Q=b-2a-3b-2c=-2a-2b-2c,
∴Q-P=-2a-2b-2c-3b+2c=-2a-5b=-... 已知二次函数y=﹣2x2+4x﹣3,如果y随x的增大而减小,那么x的取值范围是( )
A. x≥1 B. x≥0 C. x≥﹣1 D. x≥﹣2
 A
【解析】【解析】
∵y=﹣2x2+4x﹣3=﹣2(x﹣1)2﹣1,∴抛物线开口向下,对称轴为x=1,∴当x≥1时,y随x的增大而减小.故选A.
A
【解析】【解析】
∵y=﹣2x2+4x﹣3=﹣2(x﹣1)2﹣1,∴抛物线开口向下,对称轴为x=1,∴当x≥1时,y随x的增大而减小.故选A. 如图,教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-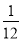 (x-4)2+3,由此可知铅球推出的距离是___________.
(x-4)2+3,由此可知铅球推出的距离是___________.

 10
【解析】【解析】
在中,令y=0,得,解得:x1=10,x2=﹣2(舍去),即铅球推出的距离是10m.故答案为:10.
10
【解析】【解析】
在中,令y=0,得,解得:x1=10,x2=﹣2(舍去),即铅球推出的距离是10m.故答案为:10. 初一(3)班共有学生50人,其中男生有21人,女生29人,若在此班上任意找一名学生,找到男生的可能性比找到女生的可能性__(填“大”或“小”).
 小
【解析】只要比较男生人数与女生人数的多少即可.
【解析】
男生人数少于女生人数,因而找到男生的可能性比找到女生的可能性小.
小
【解析】只要比较男生人数与女生人数的多少即可.
【解析】
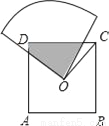
男生人数少于女生人数,因而找到男生的可能性比找到女生的可能性小. 如图,O是边长为a的正方形ABCD的中心,将一块半径足够长、圆心为直角的扇形纸板的圆心放在O点处,并将纸板的圆心绕O旋转,则正方形ABCD被纸板覆盖部分的面积为( )
A.  a2 B.
a2 B.  a2 C.
a2 C.  a2 D.
a2 D. 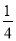 a
a
 B
【解析】【解析】
扇形的半径交AD于E,交CD于F,连结OD,如图.
∵四边形ABCD为正方形,∴OD=OC,∠COD=90°,∠ODA=∠OCD=45°.
∵∠EOF=90°,即∠EOD+∠DOF=90°,∠DOF+∠COF=90°,∴∠EOD=∠FOC.
在△ODE和△OCF中,∵∠ODE=∠OCF,OD=OC,∠EOD=∠COF,∴△ODE≌△OCF,∴S△OD...
B
【解析】【解析】
扇形的半径交AD于E,交CD于F,连结OD,如图.
∵四边形ABCD为正方形,∴OD=OC,∠COD=90°,∠ODA=∠OCD=45°.
∵∠EOF=90°,即∠EOD+∠DOF=90°,∠DOF+∠COF=90°,∴∠EOD=∠FOC.
在△ODE和△OCF中,∵∠ODE=∠OCF,OD=OC,∠EOD=∠COF,∴△ODE≌△OCF,∴S△OD... 
