��Ŀ����
��ͼ����ƽ���ı���ABCD�У���BAD��ƽ����AE��BC�ڵ�E����BE��3.��ƽ���ı���ABCD���ܳ���16����EC�ij�Ϊ________��

 2
�������������������ƽ���ı��ε����ʺ���֪����֤����BAE=��BEA��֤��AB=BE=3�����AB+BC=8���ó�BC=5�����ɵó�EC�ij������ı���ABCD��ƽ���ı��Σ���AD��BC��AB=CD��AD=BC�����AEB=��DAE��
��ƽ���ı���ABCD���ܳ���16����AB+BC=8����AE�ǡ�BAD��ƽ���ߣ����BAE=��DAE��
���BAE=��AEB����AB=BE=3����...
2
�������������������ƽ���ı��ε����ʺ���֪����֤����BAE=��BEA��֤��AB=BE=3�����AB+BC=8���ó�BC=5�����ɵó�EC�ij������ı���ABCD��ƽ���ı��Σ���AD��BC��AB=CD��AD=BC�����AEB=��DAE��
��ƽ���ı���ABCD���ܳ���16����AB+BC=8����AE�ǡ�BAD��ƽ���ߣ����BAE=��DAE��
���BAE=��AEB����AB=BE=3����...
Ҫʹ����ʽ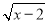 ������,��x��ȡֵ��Χ��( )
������,��x��ȡֵ��Χ��( )
A.x��2 B.x��-2 C.x��-2 D.x��2
 A��
��������
����������������⣬��
x-2��0��
��ã�x��2��
��ѡA��
A��
��������
����������������⣬��
x-2��0��
��ã�x��2��
��ѡA�� ��ͼ���ڡ�ABC�У���ACB=90�㣬M��N�ֱ���AB��AC���е㣬�ӳ�BC����D��ʹCD=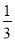 BD������DM��DN��MN����AB=6����DN=___��
BD������DM��DN��MN����AB=6����DN=___��
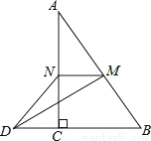
 3��
���������������������CM��������������λ�߶����õ�NM=CB��MN��BC����CD=BD���ɵ�MN=CD������MN��BC���ɵ��ı���DCMN��ƽ���ı��Σ�����DN=CM������ֱ�������ε����ʵõ�CM=AB=3�����ɵ�DN=3��
3��
���������������������CM��������������λ�߶����õ�NM=CB��MN��BC����CD=BD���ɵ�MN=CD������MN��BC���ɵ��ı���DCMN��ƽ���ı��Σ�����DN=CM������ֱ�������ε����ʵõ�CM=AB=3�����ɵ�DN=3�� ���Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮��֤���е��ı���EFGH��ƽ���ı��Σ�
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
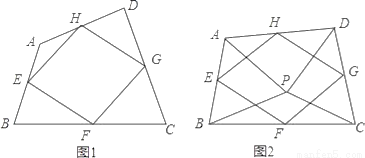
 ��1��֤������������2���ı���EFGH�����Σ�֤������������3���ı���EFGH��������.
�������������������1����ͼ1�У�����BD��������������λ�߶���ֻҪ֤��EH��FG��EH=FG���ɣ�
��2���ı���EFGH�����Σ���֤����APC�ա�BPD���õ�AC=BD����֤��EF=FG���ɣ�
��3���ı���EFGH�������Σ�ֻҪ֤����EHG=90�㣬���á�APC�ա�BPD���á�ACP=��B...
��1��֤������������2���ı���EFGH�����Σ�֤������������3���ı���EFGH��������.
�������������������1����ͼ1�У�����BD��������������λ�߶���ֻҪ֤��EH��FG��EH=FG���ɣ�
��2���ı���EFGH�����Σ���֤����APC�ա�BPD���õ�AC=BD����֤��EF=FG���ɣ�
��3���ı���EFGH�������Σ�ֻҪ֤����EHG=90�㣬���á�APC�ա�BPD���á�ACP=��B... ��֪ƽ���ı���ABCD�У�CEƽ�֡�BCD�ҽ�AD�ڵ�E��AF��CE���ҽ�BC�ڵ�F��
��1����֤����ABF�ա�CDE��
��2����ͼ������1=65�㣬���B�Ĵ�С��
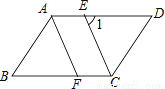
 ��1��֤������������2��50�㣮
�������������������1����ƽ���ı��ε����ʵó�AB=CD��AD��BC����B=��D���ó���1=��DCE��֤����AFB=��1����AAS֤����ABF�ա�CDE���ɣ���2���ɣ�1���á�1=��DCE=65�㣬��ƽ���ı��ε����ʺ��������ڽǺͶ������ɵó������
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AB=CD��AD��BC����B=��D�� ���1=��DCE...
��1��֤������������2��50�㣮
�������������������1����ƽ���ı��ε����ʵó�AB=CD��AD��BC����B=��D���ó���1=��DCE��֤����AFB=��1����AAS֤����ABF�ա�CDE���ɣ���2���ɣ�1���á�1=��DCE=65�㣬��ƽ���ı��ε����ʺ��������ڽǺͶ������ɵó������
�����������1�����ı���ABCD��ƽ���ı��Σ� ��AB=CD��AD��BC����B=��D�� ���1=��DCE... ��ͼ�����ı���ABCD�У��Խ���AC��BD�ཻ�ڵ�E����CBD��90�㣬BC��4��BE��ED��3��AC��10�����ı���ABCD�����Ϊ( )
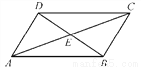
A. 6 B. 12 C. 20 D. 24
 D
�������������������Rt��CBE�У��ɹ��ɶ��������EC=5������AC=10������AE=EC=5.���ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��ο��ж��ı���ABCD��ƽ���ı��Σ�����ƽ���ı���ABCD�����ΪBC��BD=4��6=24���ʴ�ѡD.
D
�������������������Rt��CBE�У��ɹ��ɶ��������EC=5������AC=10������AE=EC=5.���ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��ο��ж��ı���ABCD��ƽ���ı��Σ�����ƽ���ı���ABCD�����ΪBC��BD=4��6=24���ʴ�ѡD. ��ͼ���ڡ�ABC�У�AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ����ı���BEDF���ܳ��ǣ� ��
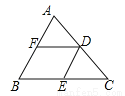
A��5 B��7 C��8 D��10
 D��
��������
�����������AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ���DE=AB=2��DF=BC=3��DE��BF��DF��BE�����ı���BEDFΪƽ���ı��Σ����ı���BEDF���ܳ�Ϊ��2��2+3��2=10����ѡD��
D��
��������
�����������AB=4��BC=6��DE��DF�ǡ�ABC����λ�ߣ���DE=AB=2��DF=BC=3��DE��BF��DF��BE�����ı���BEDFΪƽ���ı��Σ����ı���BEDF���ܳ�Ϊ��2��2+3��2=10����ѡD�� ��ͬһ����ϵ�У�һ�κ���y=ax+b����κ���y=ax2+b�Ĵ���ͼ���ǣ�������
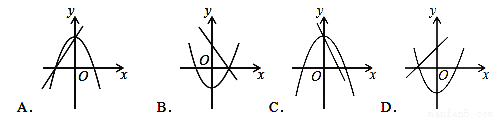
A. A B. B C. C D. D
 C
���������⣺A����һ�κ���y=ax+b��ͼ��ɵã�a��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������ϣ���A����
B����һ�κ���y=ax+b��ͼ��ɵã�a��0��b��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������£����������������㣬��B����
C����һ�κ���y=ax+b��ͼ��ɵã�a��0��b��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������£����������������㣬��C��ȷ��...
C
���������⣺A����һ�κ���y=ax+b��ͼ��ɵã�a��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������ϣ���A����
B����һ�κ���y=ax+b��ͼ��ɵã�a��0��b��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������£����������������㣬��B����
C����һ�κ���y=ax+b��ͼ��ɵã�a��0��b��0����ʱ���κ���y=ax2+b��ͼ��Ӧ�ÿ������£����������������㣬��C��ȷ��... �����¼��У���������¼����ǣ�������
A. ͨ��ˮ���ȵ�100��ʱ����
B. ����Т��ij���������£����Ϊ��150��
C. һ������װ��5������������һ���Ǻ���
D. �����Ա�ڷ�������Ͷ��һ�Σ�δͶ��
 D
����������������������ѧ������¼����Ȼ�¼������壬A��Ȼ�������DZ�Ȼ�¼���Bһ�����ᷢ�����DZ�Ȼ�¼���Cһ���ᷢ�����DZ�Ȼ�¼���D ����Ͷ��һ��δͶ���ǿ��ܷ����ģ���������¼�.��ѡD.
D
����������������������ѧ������¼����Ȼ�¼������壬A��Ȼ�������DZ�Ȼ�¼���Bһ�����ᷢ�����DZ�Ȼ�¼���Cһ���ᷢ�����DZ�Ȼ�¼���D ����Ͷ��һ��δͶ���ǿ��ܷ����ģ���������¼�.��ѡD. 
