题目内容
如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为（ ）
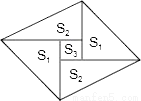
A. 4S1 B. 4S2 C. 4S2+S3 D. 3S1+4S3
A
【解析】试题分析：设等腰直角三角形的直角边长为a，中间小正方形的边长为b，则另两个直角三角形的边长分别为a-b，a+b，所以S1=，S2=，S3=，平行四边形的面积=2S1+2S2+S3=++=2=4S1，故答案选A.
星级口算天天练系列答案
芒果教辅达标测试卷系列答案如图，下列条件能保证△ABC≌△ADC的是：①AB=AD，BC=DC；②∠1=∠3，∠4=∠2；③∠1=∠2，∠4=∠3；④∠1=∠2，AB=AD；⑤∠1=∠2，BC=DC．（ ）
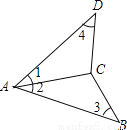
A. ①②③④⑤ B. ①②③④ C. ①③④ D. ①③④⑤
C
【解析】∵在△ABC和△ADC中，AC=AC，
∴当添加条件：①AB=AD，BC=DC时，可由“SSS”得到△ABC≌△ADC；
当添加条件：②∠1=∠3，∠4=∠2时，不能得到△ABC≌△ADC；
当添加条件：③∠1=∠2，∠4=∠3时，可由“AAS”得到△ABC≌△ADC；
当添加条件：④∠1=∠2，AB=AD时，可由“SAS”得到△ABC≌△ADC；
... 要使代数式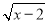
有意义,则x的取值范围是( )
A.x≥2 B.x≥-2 C.x≤-2 D.x≤2
A．
【解析】
试题分析：根据题意，得
x-2≥0，
解得，x≥2；
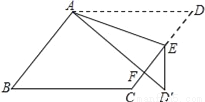
故选A． 如图，在?ABCD中，E为边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F．若∠B=52°，∠DAE=20°，则∠FED′的大小为________．
36°
【解析】试题分析：∵四边形ABCD是平行四边形，
∴∠D＝∠B＝52°，
由折叠的性质得：∠D′＝∠D＝52°，∠EAD′＝∠DAE＝20°，
∴∠AEF＝∠D＋∠DAE＝52°＋20°＝72°，∠AED′＝180°－∠EAD′－∠D′＝108°，
∴∠FED′＝108°－72°＝36°；
故答案为：36°． 如图，?ABCD的对角线AC，BD相交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC的周长为( )
A. 13 B. 17 C. 20 D. 26
B
【解析】试题分析：由平行四边形的性质得出OA=OC=3，OB=OD=6，BC=AD=8，即可求出△OBC的周长．
【解析】
∵四边形ABCD是平行四边形，
∴OA=OC=3，OB=OD=6，BC=AD=8，
∴△OBC的周长=OB+OC+AD=3+6+8=17．
故选：B． 如图，□ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N。
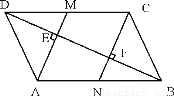
（1）求证：四边形CMAN是平行四边形。
（2）已知DE＝4，FN＝3，求BN的长。
（1）详见解析；（2）5．
【解析】
试题分析：（1）通过AE⊥BD，CF⊥BD证明AE∥CF，再由四边形ABCD是平行四边形得到AB∥CD，由两组对边分别平行的四边形是平行四边形可证得四边形CMAN是平行四边形；（2）证明△MDE≌∠NBF，根据全等三角形的性质可得DE=BF=4，再由勾股定理得BN=5．
试题解析：（1）证明：∵AE⊥BD CF⊥BD
∴AE∥CF
... 如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD=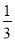
BD，连接DM、DN、MN．若AB=6，则DN=___．
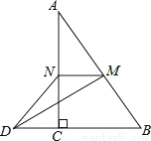
3．
【解析】试题分析：连接CM，根据三角形中位线定理得到NM=CB，MN∥BC，又CD=BD，可得MN=CD，又由MN∥BC，可得四边形DCMN是平行四边形，所以DN=CM，根据直角三角形的性质得到CM=AB=3，即可得DN=3． 我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
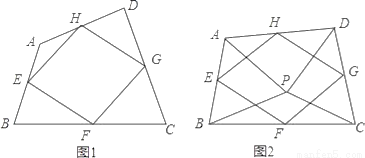
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）
（1）证明见解析；（2）四边形EFGH是菱形，证明见解析；（3）四边形EFGH是正方形.
【解析】试题分析：（1）如图1中，连接BD，根据三角形中位线定理只要证明EH∥FG，EH=FG即可．
（2）四边形EFGH是菱形．先证明△APC≌△BPD，得到AC=BD，再证明EF=FG即可．
（3）四边形EFGH是正方形，只要证明∠EHG=90°，利用△APC≌△BPD，得∠ACP=∠B... 在同一坐标系中，一次函数y=ax+b与二次函数y=ax2+b的大致图象是（ ）
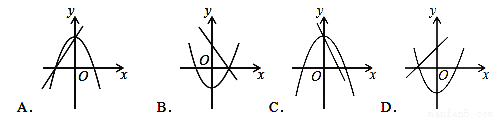
A. A B. B C. C D. D
C
【解析】解：A．由一次函数y=ax+b的图象可得：a＞0，此时二次函数y=ax2+b的图象应该开口向上，故A错误；
B．由一次函数y=ax+b的图象可得：a＜0，b＞0，此时二次函数y=ax2+b的图象应该开口向下，顶点的纵坐标大于零，故B错误；
C．由一次函数y=ax+b的图象可得：a＜0，b＞0，此时二次函数y=ax2+b的图象应该开口向下，顶点的纵坐标大于零，故C正确；...