题目内容
分解因式:
(1)-a3-2a2-a.
(2)3(x-2y)2-27(3x+y)2.
(3)(a+b)2+(a-b)2-4ab.
(1)-a3-2a2-a.
(2)3(x-2y)2-27(3x+y)2.
(3)(a+b)2+(a-b)2-4ab.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)根据提公因式,公式法,可分解因式;
(2)根据提公因式法,平方差公式,可分解因式;
(3)根据完全平方公式,提公因式,公式法,可分解因式.
(2)根据提公因式法,平方差公式,可分解因式;
(3)根据完全平方公式,提公因式,公式法,可分解因式.
解答:解:(1)原式=-a(a2+2a+1)=-a(a+1)2;
(2)原式=3[(x-2y)2-9(3x+y)2]
=3[(x-2y)+3(3x+y)][(x-2y)-3(3x+y)]
=3[10x+y][-8x-5y]
=-3(10x+y)(8x+5y);
(3)原式=a2+2ab+b2+a2-2ab+b2-4ab
=2a2-4ab+2b2
=2(a2-2ab+b2)
=2(a-b)2.
(2)原式=3[(x-2y)2-9(3x+y)2]
=3[(x-2y)+3(3x+y)][(x-2y)-3(3x+y)]
=3[10x+y][-8x-5y]
=-3(10x+y)(8x+5y);
(3)原式=a2+2ab+b2+a2-2ab+b2-4ab
=2a2-4ab+2b2
=2(a2-2ab+b2)
=2(a-b)2.
点评:本题考查了因式分解,利用了提公因式法,公式法分解因式,注意分解要彻底.

练习册系列答案
相关题目
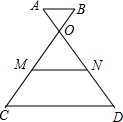 如图,已知AB∥CD,OA:OD=1:4,点M、N分别是OC、OD的中点,则△ABO与四边形CDNM的面积比为( )
如图,已知AB∥CD,OA:OD=1:4,点M、N分别是OC、OD的中点,则△ABO与四边形CDNM的面积比为( )| A、1:4 | B、1:8 |
| C、1:12 | D、1:16 |
 如图,已知CD垂直平分AB,BE垂直平分AC,求证:AB=AC.
如图,已知CD垂直平分AB,BE垂直平分AC,求证:AB=AC.