题目内容
(2x+1)(2x-1)等于( )
A. 4x2-1 B. 2x2-1 C. x2-1 D. 2x2+1
 A
【解析】根据平方差公式可得:(2x+1)(2x-1)=4x2-1,故选A.
A
【解析】根据平方差公式可得:(2x+1)(2x-1)=4x2-1,故选A.
练习册系列答案
相关题目
到一个角的两边距离相等的点都在_________。
 这个角的平分线上
【解析】根据定义可知:到一个角的两边距离相等的点在这个角的平分线上、角平分线上的点到这个角的两边的距离相等。
这个角的平分线上
【解析】根据定义可知:到一个角的两边距离相等的点在这个角的平分线上、角平分线上的点到这个角的两边的距离相等。 (2x-y 2 ) 2 等于( )
A. 2x2-4xy 2+y4 B. 4x2-2xy 2+y4 C. 4x2-4xy 2+y4 D. 4x2-xy 2+y4
 C
【解析】根据完全平方公式可得:(2x-y 2 ) 2 =4x2-4xy 2+y4 ,故选C.
C
【解析】根据完全平方公式可得:(2x-y 2 ) 2 =4x2-4xy 2+y4 ,故选C. [(c2)2+(a2)2][(c2)2-(a2)2]等于( )
A. c -a2 B. 4c2 -a8 C. c8 -a8 D. c2 -a4
 C
【解析】根据平方差公式和幂的乘方法则可得:[(c2)2+(a2)2][(c2)2-(a2)2]= =c8 -a8,故选C.
C
【解析】根据平方差公式和幂的乘方法则可得:[(c2)2+(a2)2][(c2)2-(a2)2]= =c8 -a8,故选C. 下面计算正确的是( )
A. (a+b)(a-b)=2a+2b B. b5 + b5 = b10 C. x5·x5 = x25 D. (y-z)(y+z)=y2-z2
 D
【解析】选项A,原式=a2-b2 ;选项 B,原式=2b5;选项C,原式=x10 ;选项D,原式= y2-z2.故选D.
D
【解析】选项A,原式=a2-b2 ;选项 B,原式=2b5;选项C,原式=x10 ;选项D,原式= y2-z2.故选D. 如图,在平面直角坐标系内,四边形OECB的顶点坐标分别是:B(2,5),C(8,5),E(10,0),点P(x,0)是线段OE上一点,设四边形BPEC的面积为S.
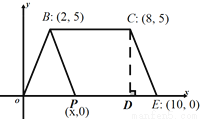
(1)过点C作CD⊥x轴于点E,则CD= , 用含x的代数式表示PE= .
(2)求S与x的函数关系.
(3)当S=30时,直接写出线段PE与PB的长.
 (1)CD=5,PE=10-x;(2)(3)PE=6,PB=
【解析】试题分析:(1)根据点D的坐标直接求得CD的长,根据点E的坐标表示出PE的长即可;(2)根据已知条件可知四边形BPEC是梯形,利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值,即可求得PE的长,过点B作BM⊥X轴于点M,在Rt△BPM中,根据勾股定理求得PB的长即可.
试题解析:
(1)CD=5,P...
(1)CD=5,PE=10-x;(2)(3)PE=6,PB=
【解析】试题分析:(1)根据点D的坐标直接求得CD的长,根据点E的坐标表示出PE的长即可;(2)根据已知条件可知四边形BPEC是梯形,利用梯形的面积公式即可求解.(2)把S=30 代入求得x的值,即可求得PE的长,过点B作BM⊥X轴于点M,在Rt△BPM中,根据勾股定理求得PB的长即可.
试题解析:
(1)CD=5,P... 若等腰三角形的一个外角为40°,则它的顶角的度数为_____.
 140°
【解析】由等腰三角形的一个外角为40°,可得这个等腰三角形的一个内角为140°,根据三角形的内角和定理可得这个角为等腰三角形的顶角,即这个等腰三角形顶角的度数为140°.
140°
【解析】由等腰三角形的一个外角为40°,可得这个等腰三角形的一个内角为140°,根据三角形的内角和定理可得这个角为等腰三角形的顶角,即这个等腰三角形顶角的度数为140°. 当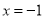 时,求分式
时,求分式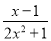 的值.
的值.
 【解析】把x=-1代入分式求值即可.
【解析】
当 时,
原式=.
故答案为: .
【解析】把x=-1代入分式求值即可.
【解析】
当 时,
原式=.
故答案为: . 当y=x+ 时,
时, 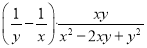 的值是_________.
的值是_________.
 -3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
-3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3. 
