题目内容
当y=x+ 时,
时, 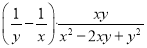 的值是_________.
的值是_________.
 -3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
-3
【解析】
=
=
∵y=x+,
∴x-y=,
∴原式==-3.
练习册系列答案
相关题目
(2x+1)(2x-1)等于( )
A. 4x2-1 B. 2x2-1 C. x2-1 D. 2x2+1
 A
【解析】根据平方差公式可得:(2x+1)(2x-1)=4x2-1,故选A.
A
【解析】根据平方差公式可得:(2x+1)(2x-1)=4x2-1,故选A. 下列式子是分式的是( )
A. 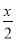 B.
B. 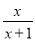 C.
C. 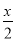 +y D.
+y D. 
 B
【解析】根据分式的定义——分母中含有字母的式子,易得B.
B
【解析】根据分式的定义——分母中含有字母的式子,易得B. 已知x=1时,分式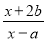 无意义,x=4时分式的值为0,求a+b的值.
无意义,x=4时分式的值为0,求a+b的值.
 -1
【解析】根据当x=1时,分式无意义,可得;根据当x=4时,分式的值为0,可得,即可求出a、b的值,最后代入求值即可.
【解析】
∵x=1时, 无意义,
∴1-a=0,
∴a=1,
∵x=4时, =0,
∴4+2b=0,
∴b=-2,
∴a+b=1+(-2)=-1.
-1
【解析】根据当x=1时,分式无意义,可得;根据当x=4时,分式的值为0,可得,即可求出a、b的值,最后代入求值即可.
【解析】
∵x=1时, 无意义,
∴1-a=0,
∴a=1,
∵x=4时, =0,
∴4+2b=0,
∴b=-2,
∴a+b=1+(-2)=-1. 已知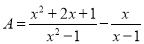 .
.
(1)化简A;
(2)当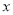 满足不等式组
满足不等式组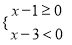 ,且
,且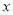 为整数时,求A的值.
为整数时,求A的值.
 (1);(2)1
【解析】试题分析:首先将分式的分子和分母进行因式分解,然后进行约分,最后根据同分母的分式减法法则得出化简的答案;根据题意求出不等式组的整数解,然后根据分式的性质求出x的值,将x的值代入化简后的式子进行计算.
试题解析:(1)原式====
(2)不等式组的解集为1≤x<3 ∵x为整数 ∴x=1或2
∵A=∴x-1≠0 即x≠1 ∴x=2
当x=2时,原...
(1);(2)1
【解析】试题分析:首先将分式的分子和分母进行因式分解,然后进行约分,最后根据同分母的分式减法法则得出化简的答案;根据题意求出不等式组的整数解,然后根据分式的性质求出x的值,将x的值代入化简后的式子进行计算.
试题解析:(1)原式====
(2)不等式组的解集为1≤x<3 ∵x为整数 ∴x=1或2
∵A=∴x-1≠0 即x≠1 ∴x=2
当x=2时,原... 计算: 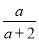 -
-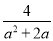 =_____.
=_____.
 【解析】因为-=-=,故答案为: .
【解析】因为-=-=,故答案为: . A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时.已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. 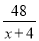 +
+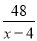 =9 B.
=9 B. 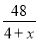 +
+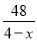 =9
=9
C. 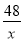 +4=9 D.
+4=9 D. 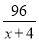 +
+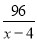 =9
=9
 A
【解析】试题分析:根据题意可以列出相应的方程,从而可以解答本题.由题意可得, .
故选:A.
A
【解析】试题分析:根据题意可以列出相应的方程,从而可以解答本题.由题意可得, .
故选:A. 已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
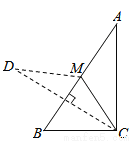
A.30° B.40° C.50° D.60°
 A.
【解析】
试题解析:如图,
∵CM是斜边AB上的中线,
∴CM=AM=AB,
∴∠A=∠MCA(设为α);
由翻折变换的性质得:∠DCM=∠MCA=α;
∵CD⊥AB,
∴∠DCA+∠A=90°,
即3α=90°,
∴∠A=α=30°.
故选A.
A.
【解析】
试题解析:如图,
∵CM是斜边AB上的中线,
∴CM=AM=AB,
∴∠A=∠MCA(设为α);
由翻折变换的性质得:∠DCM=∠MCA=α;
∵CD⊥AB,
∴∠DCA+∠A=90°,
即3α=90°,
∴∠A=α=30°.
故选A. 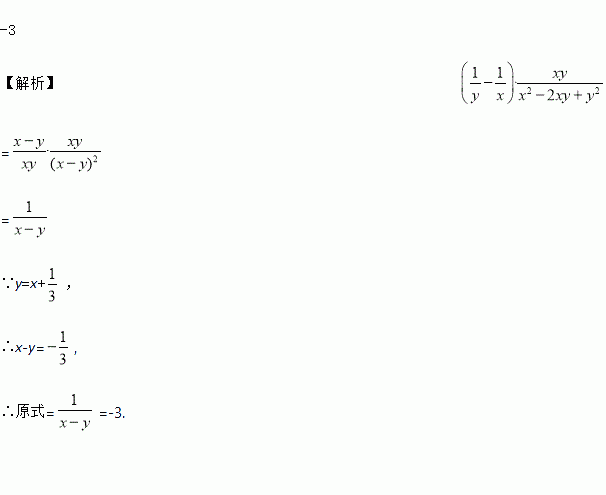

 、
、 是
是 中
中 边上的任意两点,
边上的任意两点, 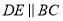 ,
,  ,则图中相等的角共有( )
,则图中相等的角共有( )
 对 B.
对 B.  对 C.
对 C.  对 D.
对 D.  对
对