题目内容
 如图,∠DCE=90°,甲、乙两个机器人同时从点C出发,分别沿CD、CE方向前进,若甲的速度为12cm/s,乙的速度为9cm/s,经过t s后,甲、乙分别到达A、B处.
如图,∠DCE=90°,甲、乙两个机器人同时从点C出发,分别沿CD、CE方向前进,若甲的速度为12cm/s,乙的速度为9cm/s,经过t s后,甲、乙分别到达A、B处.(1)求
| AC |
| BC |
(2)t为何值时,AB=60cm?
考点:勾股定理
专题:
分析:(1)根据路程=速度×时间,用含t的式子分别表示出AC,BC,再约分计算即可求解;
(2)由AB=60cm,根据勾股定理得到关于t的方程,解方程即可求解.
(2)由AB=60cm,根据勾股定理得到关于t的方程,解方程即可求解.
解答:解:(1)∵甲、乙两个机器人同时从点C出发,分别沿CD、CE方向前进,若甲的速度为12cm/s,乙的速度为9cm/s,
∴经过t s后,AC=12t,BC=9t,
∴
=
=
.
故
的值是
;
(2)根据勾股定理可得,
AC2+BC2=AB2,
即(12t)2+(9t)2=602,
解得t=±4(负值舍去).
故t为4s时,AB=60cm.
∴经过t s后,AC=12t,BC=9t,
∴
| AC |
| BC |
| 12t |
| 9t |
| 4 |
| 3 |
故
| AC |
| BC |
| 4 |
| 3 |
(2)根据勾股定理可得,
AC2+BC2=AB2,
即(12t)2+(9t)2=602,
解得t=±4(负值舍去).
故t为4s时,AB=60cm.
点评:考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.同时考查了路程=速度×时间的知识点,以及方程思想的运用.

练习册系列答案
相关题目
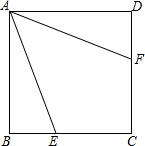 如图所示,正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF面积为y,EC为x.求y与x之间函数关系并画出这个函数图象.
如图所示,正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF面积为y,EC为x.求y与x之间函数关系并画出这个函数图象.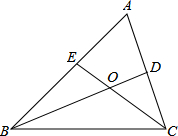 如图,∠A=60°,BD、CE是△ABC的角平分线,求证:BC=BE+CD.
如图,∠A=60°,BD、CE是△ABC的角平分线,求证:BC=BE+CD. 如图,在△ABC中,DE∥BC,且AD=3,DB=2.写出图中的相似三角形,并指出其相似比.
如图,在△ABC中,DE∥BC,且AD=3,DB=2.写出图中的相似三角形,并指出其相似比.