题目内容
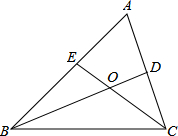 如图,∠A=60°,BD、CE是△ABC的角平分线,求证:BC=BE+CD.
如图,∠A=60°,BD、CE是△ABC的角平分线,求证:BC=BE+CD.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:在BC上找到F使得BF=BE,易证∠BOE=∠COD=60°,即可证明△BOE≌△BOF,可得∠BOF=∠BOE=60°,即可证明△OCF≌△OCD,可得CF=CD,根据BC=BF+CF即可解题.
解答:证明:在BC上找到F使得BF=BE,
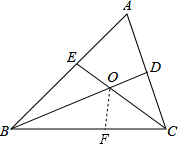
∵∠A=60°,BD、CE是△ABC的角平分线,
∴∠BOC=180°-
(∠ABC+∠ACB)=180°-
(180°-∠A)=120°,
∴∠BOE=∠COD=60°,
在△BOE和△BOF中,
,
∴△BOE≌△BOF,(SAS)
∴∠BOF=∠BOE=60°,
∴∠COF=∠BOC-∠BOF=60°,
在△OCF和△OCD中,
,
∴△OCF≌△OCD(ASA),
∴CF=CD,
∵BC=BF+CF,
∴BC=BE+CD.

∵∠A=60°,BD、CE是△ABC的角平分线,
∴∠BOC=180°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOE=∠COD=60°,
在△BOE和△BOF中,
|
∴△BOE≌△BOF,(SAS)
∴∠BOF=∠BOE=60°,
∴∠COF=∠BOC-∠BOF=60°,
在△OCF和△OCD中,
|
∴△OCF≌△OCD(ASA),
∴CF=CD,
∵BC=BF+CF,
∴BC=BE+CD.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△OCF≌△OCD是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
用配方法解方程
x2-3x+
=0,配方正确的是( )
| 1 |
| 2 |
| 7 |
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 如图,点C在AB上,且AC=
如图,点C在AB上,且AC= 如图,在△ABC中,CD⊥AB于D,且AC=4cm,BC=3cm,AB=5cm,指出图中各对相似三角形及其相似比.
如图,在△ABC中,CD⊥AB于D,且AC=4cm,BC=3cm,AB=5cm,指出图中各对相似三角形及其相似比. 如图所示,在Rt△ABC中,∠BAC=90°,点D,E在BC上,且BE=AB,CD=AC,求∠DAE的度数.
如图所示,在Rt△ABC中,∠BAC=90°,点D,E在BC上,且BE=AB,CD=AC,求∠DAE的度数. 如图,∠DCE=90°,甲、乙两个机器人同时从点C出发,分别沿CD、CE方向前进,若甲的速度为12cm/s,乙的速度为9cm/s,经过t s后,甲、乙分别到达A、B处.
如图,∠DCE=90°,甲、乙两个机器人同时从点C出发,分别沿CD、CE方向前进,若甲的速度为12cm/s,乙的速度为9cm/s,经过t s后,甲、乙分别到达A、B处. 已知△ABC中,∠C=90°,∠A=40°,CD是AB边上的高,CE是∠BCA的角平分线,分别交AB于点D、E.求∠ECD的度数.
已知△ABC中,∠C=90°,∠A=40°,CD是AB边上的高,CE是∠BCA的角平分线,分别交AB于点D、E.求∠ECD的度数.