题目内容
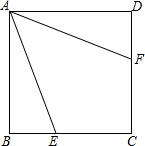 如图所示,正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF面积为y,EC为x.求y与x之间函数关系并画出这个函数图象.
如图所示,正方形ABCD中,E是BC边上的点,F是CD边上的点,且AE=AF,AB=4,设△AEF面积为y,EC为x.求y与x之间函数关系并画出这个函数图象.考点:全等三角形的判定与性质,根据实际问题列二次函数关系式,正方形的性质
专题:
分析:连接EF,根据AB,CE长度即可求得S△AEF的值,即可解题.
解答:解:连接EF,

在RT△ABE和RT△ADF中,
,
∴RT△ABE≌RT△ADF(HL),
∴BE=DF,
∵CE=x,∴BE=4-x,
∴S△AEF=16-S△ABE-S△ADF-S△CEF=16-
×4×(4-x)-
×4×(4-x)-
x2
=-
x2+2x+8.
画出图形为:

顶点A坐标(2,10),与y轴交点为B(0,8).

在RT△ABE和RT△ADF中,
|
∴RT△ABE≌RT△ADF(HL),
∴BE=DF,
∵CE=x,∴BE=4-x,
∴S△AEF=16-S△ABE-S△ADF-S△CEF=16-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
画出图形为:

顶点A坐标(2,10),与y轴交点为B(0,8).
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证RT△ABE≌RT△ADF是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点C在AB上,且AC=
如图,点C在AB上,且AC= 如图,在△ABC中,CD⊥AB于D,且AC=4cm,BC=3cm,AB=5cm,指出图中各对相似三角形及其相似比.
如图,在△ABC中,CD⊥AB于D,且AC=4cm,BC=3cm,AB=5cm,指出图中各对相似三角形及其相似比. 如图,∠DCE=90°,甲、乙两个机器人同时从点C出发,分别沿CD、CE方向前进,若甲的速度为12cm/s,乙的速度为9cm/s,经过t s后,甲、乙分别到达A、B处.
如图,∠DCE=90°,甲、乙两个机器人同时从点C出发,分别沿CD、CE方向前进,若甲的速度为12cm/s,乙的速度为9cm/s,经过t s后,甲、乙分别到达A、B处.