题目内容
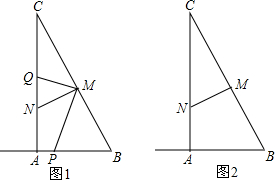
1.如图,在Rt△ABC中,∠A=90°,∠C=30°,AB=$4\sqrt{3}$,M是边BC的中点,MN⊥BC交AC于点N,动点P从点B出发沿射线BA以每秒$\sqrt{3}$个单位的速度运动,同时,动点Q从点N出发沿射线NC运动,且始终保持MQ⊥MP,设运动时间为t秒(t>0).(1)①以图1为例,求证:△PMB∽△QNM;
②在图2中,当动点P运动到BA的延长线上时,请画出满足条件的图形,并判断①的结论是否成立(不再证明)?
(2)求动点Q的运动速度;
(3)连接PQ,探求BP2,PQ2,CQ2三者之间的数量关系,以图1为例说明理由.
分析 (1)①通过垂直的定义、直角三角形中的两个锐角互余以及等量代换,可以证得△PBM与△QNM中的两个角对应相等,所以这两个三角形一定相似;
②根据题意画出图形,与①的方法类似证明即可;
(2)根据△PBM∽△QNM的对应边成比例可以求得NQ的长,即Q一分钟移动的距离,即点Q的速度;
(3)PQ2=BP2+CQ2.作辅助线延长QM至点D,使MD=MQ.连接PD、BD构建平行四边形BDCQ.根据平行四边形的对边平行且相等推知BD∥CQ,BD=CQ;然后在直角三角形BPD中利用勾股定理求得PD2=BP2+BD2=BP2+CQ2;最后利用线段垂直平分线的性质知PQ=PD,所以由等量代换证得该结论.
解答 (1)证明:①△PBM∽△QNM.
理由如下:如图1,∵MQ⊥MP,MN⊥BC,
∴∠PMB+∠PMN=90°,∠QMN+∠PMN=90°,
∴∠PMB=∠QMN,
∵∠PBM+∠C=90°,QNM+∠C=90°,
∴∠PBM=∠QNM,
∴△PBM∽△QNM; ②,①的结论成立,证明方法与①相同;
②,①的结论成立,证明方法与①相同;
(2)解:∵∠BAC=90°,∠ABC=60°,
∴BC=2AB=8$\sqrt{3}$cm.
又∵MN垂直平分BC,
∴BM=CM=4$\sqrt{3}$cm.
∵∠C=30°,
∴MN=$\frac{\sqrt{3}}{3}$CM=4cm;
①设Q点的运动速度为vcm/s.
如图1,当0<t<4时,由(1)知△PBM∽△QNM.
∴$\frac{NQ}{BP}$$\frac{MN}{MB}$,即$\frac{vt}{\sqrt{3}t}$=$\frac{4}{4\sqrt{3}}$,
∴v=1,
如图2,当t≥4时,同理可得v=1.
综上所述,Q点运动速度为1cm/s;
(3)PQ2=BP2+CQ2.
证明如下:如图1,延长QM至点D,使MD=MQ.连接PD、BD,BQ,CD
∵BC、DQ互相平分,
∴四边形BDCQ为平行四边形,
∴BD∥CQ,BD=CQ;
又∵∠BAC=90°,
∴∠PBD=90°,
∴PD2=BP2+BD2=BP2+CQ2,
∵PM垂直平分DQ,
∴PQ=PD,
∴PQ2=BP2+CQ2.
点评 本题考查了相似三角形的判定与性质,以及平行四边形知识和线段垂直平分线知识综合应用,利用时间t正确表示出题目中线段的长度是解题的关键.

 如图,△DEF是△ABC沿BC方向平移后的图形,判断S四边形ABEG与S四边形FCGD的大小关系,并说明理由.
如图,△DEF是△ABC沿BC方向平移后的图形,判断S四边形ABEG与S四边形FCGD的大小关系,并说明理由. 如图,把一张长方形纸片ABCD沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上.
如图,把一张长方形纸片ABCD沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上.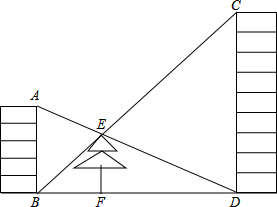 如图,在高5m的房顶A处望一楼的底部D,视线刚好过小树的顶端E,又从楼顶C处望房顶部B,视线也正好过小树的顶端E,测得小树高4m,求楼高CD.
如图,在高5m的房顶A处望一楼的底部D,视线刚好过小树的顶端E,又从楼顶C处望房顶部B,视线也正好过小树的顶端E,测得小树高4m,求楼高CD.