题目内容
6.已知m,n为数轴上在原点两侧且到原点距离相等的两个点所表示的数,且满足(m+4)2-(n+4)2=16,求m2+n2-$\frac{m}{n}$的值.分析 根据m,n为数轴上在原点两侧且到原点距离相等的两个点所表示的数,可知m,n互为相反数,则(m+4)2-(n+4)2=16可变形为(m+4)2-(-m+4)2=16,解得m的值,进一步得到n的值,再代入即可求解.
解答 解:∵m,n为数轴上在原点两侧且到原点距离相等的两个点所表示的数,
∴m,n互为相反数,
∴(m+4)2-(n+4)2=16可变形为(m+4)2-(-m+4)2=16,
解得m=1,
则n=-1,
则m2+n2-$\frac{m}{n}$=1+1+1=3.
点评 考查了代数式求值,数轴,本题关键是理解m,n互为相反数并且解方程求得m,n的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设|x-3|+$\sqrt{y+4}$=0,则(x+y)2015的值为( )
| A. | -1 | B. | 3 | C. | 22015 | D. | -22015 |
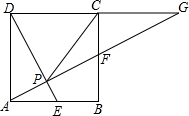 如图,正方形ABCD中,E、F分别是AB、BC的中点,AF与DE相交于点P,延长AF交DC延长线于点G
如图,正方形ABCD中,E、F分别是AB、BC的中点,AF与DE相交于点P,延长AF交DC延长线于点G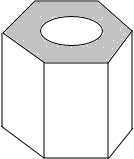 某五金厂生产的螺母形状如图所示
某五金厂生产的螺母形状如图所示