题目内容
7.计算:(1)(4×106)×(5×107)×(3×105);
(2)$\frac{2}{3}$a3b2•(-$\frac{3}{2}$ab2)2;
(3)3a2b3×(-$\frac{1}{6}$a3b4)×4abc2;
(4)-2a3bc•(-ab2)•(-ab2)2;
(5)$\frac{5}{8}$[(a+b)(a-b)]4•$\frac{4}{9}$(a+b)4(b-a)5.
分析 (1)先变形为(4×5×3)×(106×107×105),再根据同底数幂的乘法法则计算即可求解;
(2)先算积的乘方,再计算单项式的乘法;
(3)根据单项式的乘法法则计算即可求解;
(4)先算积的乘方,再根据单项式的乘法法则计算即可求解;
(5)先算积的乘方,再计算单项式的乘法,注意整体思想的应用.
解答 解:(1)(4×106)×(5×107)×(3×105)
=(4×5×3)×(106×107×105)
=60×1018
=6×1019;
(2)$\frac{2}{3}$a3b2•(-$\frac{3}{2}$ab2)2;
=$\frac{2}{3}$a3b2•$\frac{9}{4}$a2b4
=$\frac{3}{2}$a5b6;
(3)3a2b3×(-$\frac{1}{6}$a3b4)×4abc2=-2a6b8c2;
(4)-2a3bc•(-ab2)•(-ab2)2;
=-2a3bc•(-ab2)•a2b4
=2a6b7c;
(5)$\frac{5}{8}$[(a+b)(a-b)]4•$\frac{4}{9}$(a+b)4(b-a)5
=$\frac{5}{8}$(a+b)4(a-b)4•$\frac{4}{9}$(a+b)4(b-a)5
=$\frac{5}{18}$(a+b)8(a-b)9.
点评 考查了整式的混合运算,熟练掌握积的乘方,同底数幂的乘法,单项式的乘法法则是解题的关键,注意整体思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设|x-3|+$\sqrt{y+4}$=0,则(x+y)2015的值为( )
| A. | -1 | B. | 3 | C. | 22015 | D. | -22015 |
 某五金厂生产的螺母形状如图所示
某五金厂生产的螺母形状如图所示 如图,△ABC中,AB=AC=8,点P是BC边上任意一点,PD⊥AB于点D,PE⊥AC于点E,且△ABC的面积是14,求PD+PE的值.
如图,△ABC中,AB=AC=8,点P是BC边上任意一点,PD⊥AB于点D,PE⊥AC于点E,且△ABC的面积是14,求PD+PE的值.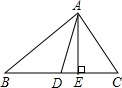 如图,AD,AE分别是△ABC的中线和高,BC=6cm,AE=4cm,则△ABC的面积为12,△ABD的面积为6.
如图,AD,AE分别是△ABC的中线和高,BC=6cm,AE=4cm,则△ABC的面积为12,△ABD的面积为6.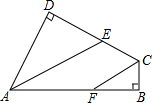 已知,如图,四边形ABCD中,AD⊥CD,BC⊥AB,AE平分∠BAD,CF平分∠DCB.AE交CD于点E,CF交AB于点F,问AE与CF是否平行?为什么?
已知,如图,四边形ABCD中,AD⊥CD,BC⊥AB,AE平分∠BAD,CF平分∠DCB.AE交CD于点E,CF交AB于点F,问AE与CF是否平行?为什么?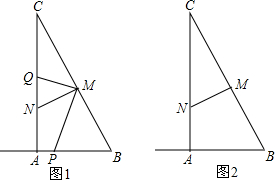
 如图,直线AB,CD,EF交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°.求:
如图,直线AB,CD,EF交于点O,AB⊥CD,OG平分∠AOE,∠FOD=28°.求: