题目内容
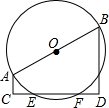AB是⊙O的直径．AC⊥CD，BD⊥CD，垂足分别为点C、D，CD交⊙O于点E、F，求证：CE=DF．考点：垂径定理,梯形中位线定理
专题：证明题
分析：作OH⊥EF于H，如图，由OH⊥EF，AC⊥CD，BD⊥CD得到AC∥OH∥BD，易得OH为梯形ABDC的中位线，根据梯形的中位线性质得CH=DH，再根据垂径定理由
OH⊥EF得到EH=FH，然后利用等量减等量差相等即可得到CE=DF．
OH⊥EF得到EH=FH，然后利用等量减等量差相等即可得到CE=DF．
解答：证明：作OH⊥EF于H，如图，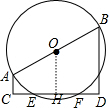
∵OH⊥EF，AC⊥CD，BD⊥CD，
∴AC∥OH∥BD，
∵OA=OB，
∴OH为梯形ABDC的中位线，
∴CH=DH，
∵OH⊥EF，
∴EH=FH，
∴CH-EH=DH-FH，
即CE=DF．
∵OH⊥EF，AC⊥CD，BD⊥CD，
∴AC∥OH∥BD，
∵OA=OB，
∴OH为梯形ABDC的中位线，
∴CH=DH，
∵OH⊥EF，
∴EH=FH，
∴CH-EH=DH-FH，
即CE=DF．
点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了梯形的中位线定理和垂径定理．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
半径为R的⊙O1和半径为r的⊙O2外切于点P，AB为两圆的外公切线，切点为A、B，连心线O2O1交圆⊙O1于C，交⊙O2于D，CA与DB的延长线相交于Q．若R=3r，求∠ABQ的度数．