题目内容
已知点(
,1)在函数y=(3m-1)x+4的图象上,
(1)求m的值;
(2)试求该函数图象与两坐标轴围成的三角形的面积.
| 1 |
| 2 |
(1)求m的值;
(2)试求该函数图象与两坐标轴围成的三角形的面积.
考点:一次函数图象上点的坐标特征
专题:计算题
分析:(1)根据一次函数图象上点的坐标特征,把点(
,1)代入y=(3m-1)x+4即可得到m的值;
(2)先(1)得到一次函数解析式为y=-6x+4,再根据坐标轴上点的坐标特征求出一次函数图象与坐标轴的两交点坐标,然后根据三角形面积公式求解.
| 1 |
| 2 |
(2)先(1)得到一次函数解析式为y=-6x+4,再根据坐标轴上点的坐标特征求出一次函数图象与坐标轴的两交点坐标,然后根据三角形面积公式求解.
解答:解:(1)把(
,1)代入y=(3m-1)x+4得(3m-1)•
+4=1,解得m=-
;
(2)一次函数解析式为y=-6x+4,
把x=0代入得y=4;把y=0代入得-6x+4=0,解得x=
,则一次函数图象与坐标轴的两交点坐标为(0,4)、(
,0),
所以该函数图象与两坐标轴围成的三角形的面积=
×4×
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
(2)一次函数解析式为y=-6x+4,
把x=0代入得y=4;把y=0代入得-6x+4=0,解得x=
| 2 |
| 3 |
| 2 |
| 3 |
所以该函数图象与两坐标轴围成的三角形的面积=
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 3 |
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
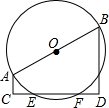 AB是⊙O的直径.AC⊥CD,BD⊥CD,垂足分别为点C、D,CD交⊙O于点E、F,求证:CE=DF.
AB是⊙O的直径.AC⊥CD,BD⊥CD,垂足分别为点C、D,CD交⊙O于点E、F,求证:CE=DF.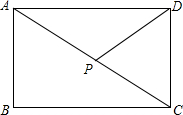 如图,矩形ABCD中,AB=3,BC=4,点P是对角线AC上的动点(不与A、C重合),设AP=x,S△CDP=y.
如图,矩形ABCD中,AB=3,BC=4,点P是对角线AC上的动点(不与A、C重合),设AP=x,S△CDP=y.