题目内容
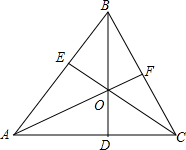 如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有
如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有考点:全等三角形的判定与性质
专题:
分析:根据△ABD≌△ACE,可得∠ABD=∠ACE,BD=CE,AE=AD,∠ADB=∠AEC,∠BEO=∠CDO,即可求得∠ABC=∠ACB,BE=CD,∠OBF=∠OCF,即可证明△BEO≌△CDO和△BEC≌△CDB,即可解题.
解答:证明:∵△ABD≌△ACE,
∴∠ABD=∠ACE,BD=CE,AE=AD,∠ADB=∠AEC,
∴∠BEO=∠CDO,
∵AB=AC,
∴∠ABC=∠ACB,BE=CD,
∴∠OBF=∠OCF,
在△BEO和△CDO中,
,
∴△BEO≌△CDO,(ASA)
∴BO=CO,EO=DO,
在△BEC和△CDB中,
,
∴△BEC≌△CDB(SAS),
∴BD=CE,

∴AF垂直平分BC,
∴∠BAF=∠CAF,BF=CF,
在△AOE和△AOD中,
,
∴△AOE≌△AOD(SAS),
在△AOB和△AOC中,
,
∴△AOB≌△AOC(SAS),
在△ABF和△ACF中,
,
∴△ABF≌△ACF(SAS),
在△OBF和△OCF中,
,
∴△OBF≌△OCF(SSS).
故答案为 6.
∴∠ABD=∠ACE,BD=CE,AE=AD,∠ADB=∠AEC,
∴∠BEO=∠CDO,
∵AB=AC,
∴∠ABC=∠ACB,BE=CD,
∴∠OBF=∠OCF,
在△BEO和△CDO中,
|
∴△BEO≌△CDO,(ASA)
∴BO=CO,EO=DO,
在△BEC和△CDB中,
|
∴△BEC≌△CDB(SAS),
∴BD=CE,

∴AF垂直平分BC,
∴∠BAF=∠CAF,BF=CF,
在△AOE和△AOD中,
|
∴△AOE≌△AOD(SAS),
在△AOB和△AOC中,
|
∴△AOB≌△AOC(SAS),
在△ABF和△ACF中,
|
∴△ABF≌△ACF(SAS),
在△OBF和△OCF中,
|
∴△OBF≌△OCF(SSS).
故答案为 6.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中找齐全等三角形不要漏解是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
某反比例函数经过点(-2,3),则下列各点不在此函数图象上的是( )
| A、(2,-3) |
| B、(3,-2) |
| C、(2,3) |
| D、(6,-1) |
 如图所示菱形ABCD,AB=6cm,∠DAB=120°,则菱形ABCD的面积为
如图所示菱形ABCD,AB=6cm,∠DAB=120°,则菱形ABCD的面积为 如图,在?ABCD中,E是AB延长线的一点,DE与边BC相交于点F,如果
如图,在?ABCD中,E是AB延长线的一点,DE与边BC相交于点F,如果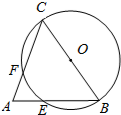 如图,在△ABC中,∠A=70°,∠B=55°,以BC为直径作⊙O,分别交AB,AC于E,F,BE与CF相等吗?为什么?
如图,在△ABC中,∠A=70°,∠B=55°,以BC为直径作⊙O,分别交AB,AC于E,F,BE与CF相等吗?为什么?