题目内容
将总长为9m的铝合金材料用来做一个“田“字型窗框,且材料完全用完.也不计接口损失,要使做成的窗框的透光面积最大,则最大的透光面积是 .
考点:二次函数的最值
专题:
分析:根据题意画出图形,进而设窗框的长为xm,则宽为:(3-x)m,表示出面积利用二次函数最值求法得出即可.
解答: 解:设窗框的长为xm,则宽为:
解:设窗框的长为xm,则宽为:
=(3-x)m,设面积为S,根据题意可得:
S=x(3-x)=-x2+3x=-(x-
)2+
.
故最大的透光面积是:
.
故答案为:
.
 解:设窗框的长为xm,则宽为:
解:设窗框的长为xm,则宽为:| 9-3x |
| 3 |
S=x(3-x)=-x2+3x=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
故最大的透光面积是:
| 9 |
| 4 |
故答案为:
| 9 |
| 4 |
点评:此题主要考查了二次函数最值求法,利用配方法求出是解题关键.

练习册系列答案
相关题目
已知点A的坐标为(-1-a2,3),那么点A一定在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
 如图,AB是⊙O的直径,D是⊙O上一点,过点A的切线与CD的延长线相交于点C,BD的延长线交AC于E,△ACD与△DCE相似吗?为什么?
如图,AB是⊙O的直径,D是⊙O上一点,过点A的切线与CD的延长线相交于点C,BD的延长线交AC于E,△ACD与△DCE相似吗?为什么?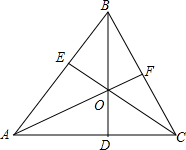 如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有
如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有