题目内容
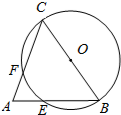 如图,在△ABC中,∠A=70°,∠B=55°,以BC为直径作⊙O,分别交AB,AC于E,F,BE与CF相等吗?为什么?
如图,在△ABC中,∠A=70°,∠B=55°,以BC为直径作⊙O,分别交AB,AC于E,F,BE与CF相等吗?为什么?考点:圆周角定理,圆心角、弧、弦的关系
专题:常规题型
分析:先利用三角形内角和定理计算出∠C=55°,则∠B=∠C,根据圆周角定理得
=
,所以
=
,然后根据圆心角、弧、弦的关系即可得到BE=CF.
 |
| CE |
 |
| BF |
 |
| CF |
 |
| BE |
解答:解:BE=CF.理由如下:
∵∠A=70°,∠B=55°,
∴∠C=180°-∠A-∠B=55°,
∴∠B=∠C,
∴
=
,
∴
=
,
∴BE=CF.
∵∠A=70°,∠B=55°,
∴∠C=180°-∠A-∠B=55°,
∴∠B=∠C,
∴
 |
| CE |
 |
| BF |
∴
 |
| CF |
 |
| BE |
∴BE=CF.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了圆心角、弧、弦的关系.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知点A的坐标为(-1-a2,3),那么点A一定在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
下列各式中,正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若分式
的值为0,则x的值为( )
| x2-6x+9 |
| x+3 |
| A、10 | B、3 | C、-3 | D、±3 |
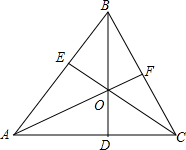 如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有
如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有
 如图,已知 AB=CD,要使△ABC≌△DCB成立,还需填加一个条件,那么这个条件可是:
如图,已知 AB=CD,要使△ABC≌△DCB成立,还需填加一个条件,那么这个条件可是: