题目内容
 如图所示菱形ABCD,AB=6cm,∠DAB=120°,则菱形ABCD的面积为
如图所示菱形ABCD,AB=6cm,∠DAB=120°,则菱形ABCD的面积为考点:菱形的性质
专题:
分析:设对角线相交于点O,根据已知条件可求出△AOB的面积,进而可求出菱形ABCD的面积.
解答: 解:设对角线相交于点O,
解:设对角线相交于点O,
∵∠DAB=120°,
∴∠ABC=60°,
∴∠ABO=30°,
∵AB=6cm,
∴AO=3cm,BO=3
cm,
∴S△AOB=
×AO•BO=
cm2,
∴菱形ABCD的面积为4×
=18
cm2.
故答案为:18
.
 解:设对角线相交于点O,
解:设对角线相交于点O,∵∠DAB=120°,
∴∠ABC=60°,
∴∠ABO=30°,
∵AB=6cm,
∴AO=3cm,BO=3
| 3 |
∴S△AOB=
| 1 |
| 2 |
9
| ||
| 2 |
∴菱形ABCD的面积为4×
9
| ||
| 2 |
| 3 |
故答案为:18
| 3 |
点评:本题考查了菱形的邻角互补的性质以及菱形面积公式的运用,题目综合性较强难度中等.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
矩形具有而菱形不一定具有的性质是( )
| A、对角线互相平分 |
| B、对边平行且相等 |
| C、对角线相等 |
| D、对角相等 |
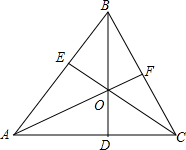 如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有
如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有 如图,已知 AB=CD,要使△ABC≌△DCB成立,还需填加一个条件,那么这个条件可是:
如图,已知 AB=CD,要使△ABC≌△DCB成立,还需填加一个条件,那么这个条件可是: