题目内容
 如图,在?ABCD中,E是AB延长线的一点,DE与边BC相交于点F,如果
如图,在?ABCD中,E是AB延长线的一点,DE与边BC相交于点F,如果| BE |
| AE |
| 3 |
| 7 |
| BF |
| FC |
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:由平行四边形的性质可得
=
,再根据已知
=
,且AE=CD+BE,代入可求得答案.
| BF |
| FC |
| BE |
| CD |
| BE |
| AE |
| 3 |
| 7 |
解答:解:∵四边形ABCD为平行四边形,
∴AB=CD,且AB∥CD,
∵
=
,
∴
=
,
∴
=
,
又∵AB∥CD,
∴
=
=
,
故答案为:
.
∴AB=CD,且AB∥CD,
∵
| BE |
| AE |
| 3 |
| 7 |
∴
| BE |
| CD+BE |
| 3 |
| 7 |
∴
| BE |
| CD |
| 3 |
| 4 |
又∵AB∥CD,
∴
| BF |
| CF |
| BE |
| CD |
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题主要考查平行四边形的性质,掌握平行四边形的对边平行且相等是解题的关键,注意平行线分线段成比例性质的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
矩形具有而菱形不一定具有的性质是( )
| A、对角线互相平分 |
| B、对边平行且相等 |
| C、对角线相等 |
| D、对角相等 |
已知点A的坐标为(-1-a2,3),那么点A一定在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若分式
的值为0,则x的值为( )
| x2-6x+9 |
| x+3 |
| A、10 | B、3 | C、-3 | D、±3 |
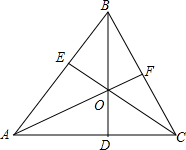 如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有
如图所示,在△ABC中,AB=AC,D、E、F分别是边AC、AB、BC上的点,O是BD、AF、CF的交点,若△ABD≌△ACE,则全等的三角形还有