题目内容
13.如图(1)所示,在△ABC中,AD⊥BC于D.(1)AE平分∠BAC,∠B=70°,∠C=34°,试求∠DAE的度数,你能把∠B,∠C,∠DAE的关系规律化吗?证明你的结论.
(2)设F为AE上任一点,当它在AE上滑动,AD变成FD,如图(2)时,结论还成立吗?当它滑动到AE的延长线上时,AD变成FD,如图(3)时,结论还成立吗?证明你的结论.
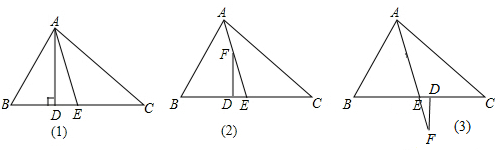
分析 (1)如图(1)先由互余计算出∠BAD=90°-∠B,再根据三角形内角和定理得到∠BAC=180°-∠B-∠C,而AE平分∠BAC,则∠BAE=$\frac{1}{2}$∠BAC,于是∠DAE=∠BAE-∠BAD=$\frac{1}{2}$(∠B-∠C),然后把∠B=70°,∠C=34°代入计算即可;
(2)如图(2),结论成立.作AH⊥BC于H,由(1)得∠HAE=$\frac{1}{2}$(∠B-∠C),根据平行线的性质易得∠DFE=∠HAE=$\frac{1}{2}$(∠B-∠C);如图(3),结论成立,方法与图(2)一样.
解答 解:(1)如图(1)
∵AD⊥BC,
∴∠ADB=90°,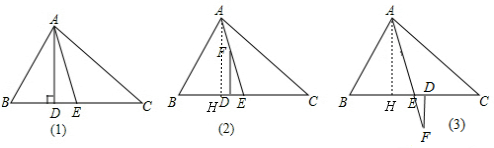
∴∠BAD=90°-∠B=90°-70°=20°,
∵∠BAC=180°-∠B-∠C=180°-70°-34°=76°,
而AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×76°=38°,
∴∠DAE=∠BAE-∠BAD=38°-20°=18°;
∠B,∠C,∠DAE的关系为∠DAE=$\frac{1}{2}$(∠B-∠C),理由如下:
∵∠BAD=90°-∠B,
∠BAC=180°-∠B-∠C,
而AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-∠B-∠C)=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$C,
∴∠DAE=∠BAE-∠BAD=90°-$\frac{1}{2}$∠B-$\frac{1}{2}$C+∠B=$\frac{1}{2}$(∠B-∠C);
(2)如图(2),结论成立.作AH⊥BC于H,由(1)得∠HAE=$\frac{1}{2}$(∠B-∠C),
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=$\frac{1}{2}$(∠B-∠C);
如图(3),结论成立.理由如下:
作AH⊥BC于H,由(1)得∠HAE=$\frac{1}{2}$(∠B-∠C),
∵AH∥FD,
∴∠DFE=∠HAE,
∴∠DFE=$\frac{1}{2}$(∠B-∠C).
点评 本题考查了三角形内角和定理:三角形内角和是180°.三角形内角和主要用在求三角形中角的度数.也考查了三角形外角性质.

 名校课堂系列答案
名校课堂系列答案| x | 617 | 618 | 619 | 620 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<617 | B. | 617<x<618 | C. | 618<x<619 | D. | 619<x<7 |
| A. | $-\frac{3}{4}$的倒数是$\frac{4}{3}$ | B. | $-\frac{1}{3}$的相反数是$\frac{1}{3}$ | C. | -|-3|=3 | D. | 以上结论都不对 |
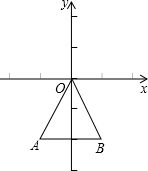 如图,△OAB三个顶点的坐标分别为O(0,0)、A(-1,-2)、B(1,-2),以B点为位似中心将△OAB放大2倍,求放大后的三角形各顶点的坐标.(提示:分两种情况)
如图,△OAB三个顶点的坐标分别为O(0,0)、A(-1,-2)、B(1,-2),以B点为位似中心将△OAB放大2倍,求放大后的三角形各顶点的坐标.(提示:分两种情况)