题目内容
8.十年后,某班学生聚会,见面时相互间均握了一次手,一共握了780次.你认为这次参加聚会的同学有40人.分析 设这次聚会的同学有x人,每名同学要握手(x-1)次,共握手x(x-1)次,但是每两名同学只握手一次,需将重复计算的握手次数去掉,即共握手$\frac{1}{2}$x(x-1)次,然后根据一共握手780次就可以列出方程解决问题.
解答 解:设这次聚会的同学有x人,
依题意得$\frac{1}{2}$x(x-1)=780,
∴x2-x-1560=0,
∴x1=40,x2=-39(负值舍去).
即:这次聚会的同学有40人.
故答案是:40.
点评 此题考查了一元二次方程的应用,该题和实际生活结合比较紧密,正确理解题意,找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.最后要判断所求的解是否符合题意,舍去不合题意的解.

练习册系列答案
相关题目
18. 如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
 如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )
如图,在综合实践活动中,小明在学校门口的点C处测得树的顶端A仰角为37°,同时测得BC=20米,则树的高AB(单位:米)为( )| A. | $\frac{20}{sin37°}$ | B. | 20tan37° | C. | $\frac{20}{tan37°}$ | D. | 20sin37° |
19.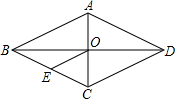 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )
 已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )
已知:如图,菱形ABCD中,对角线AC与BD相交于点O,E是BC中点E,AD=6cm,则OE的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
3.已知二次函数y=kx2-7x-7的图象和x轴有交点,则k的取值范围是( )
| A. | k>-$\frac{7}{4}$ | B. | k≥-$\frac{7}{4}$ | C. | k≥-$\frac{7}{4}$且k≠0 | D. | k>-$\frac{7}{4}$且k≠0 |
20.下列等式中,不成立的是( )
| A. | |-2|3=|2|3 | B. | (-2)2=22 | C. | (-2)3=-23 | D. | (-2)4=-24 |