题目内容

1．在平面直角坐标系中，点P（a-2，a+4）在二四象限的角平分线上，则a2013=-1．

分析 由点P（a-2，a+4）在二四象限的角平分线上可得a-2与a+4互为相反数，从而可求得a的值，从而求得a2013的值．

解答 解：∵在平面直角坐标系中，点P（a-2，a+4）在二四象限的角平分线上．
∴（a-2）+（a+4）=0．
解得，a=-1．
∴a2013=（-1）2013=-1．
故答案为：-1．

点评 本题主要考查平面直角坐标系中关于二四象限角平分线的知识，关键是明确二四象限角平分线上的点的横纵坐标互为相反数．

练习册系列答案
相关题目
11．一个三角形的三个外角之比为3：2：3，则这个三角形是（　　）
A．等腰三角形B．直角三角形
C．等腰直角三角形D．等腰三角形或直角三角形
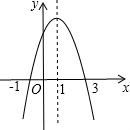12．结合二次函数y=-$\frac{2}{3}$x2+$\frac{4}{3}$x+2的图象图回答：
（1）当x=-1或3时，y=0
（2）当-1＜x＜3时，y＞0
（3）当x＜-1或x＞3时，y＜0．
9．将二次函数y=-2（x-1）2-1的图象先向右平移一个单位，再沿x轴翻折到x轴上方，然后向右平移一个单位，再沿y轴翻折到，再向右平移一个单位，再沿x轴翻折…以此类推，如果把向右平移一个单位再沿坐标轴翻折一次记作1次变换，那么二次函数y=-2（x-1）2-1的图象经过2015次变换后，得到的图象的函数解析式为y=-2（x+2）2-1．
16．把下列各数填入它所属的集合内：
-7.2，-42，5，0.1，$\frac{22}{7}$，-5$\frac{1}{2}$，0，-6
非负数集合{                                                …}
负分数集合{                                                …}
整数集合 {                                                 …}．
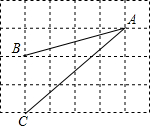6．如图，在6×5的矩形网格中，每格小正方形的边长都是1，若△ABC的三个顶点在图中相应的格点上，则sin∠BAC的值为$\frac{8\sqrt{17}}{85}$．
13．如图（1）所示，在△ABC中，AD⊥BC于D．
（1）AE平分∠BAC，∠B=70°，∠C=34°，试求∠DAE的度数，你能把∠B，∠C，∠DAE的关系规律化吗？证明你的结论．
（2）设F为AE上任一点，当它在AE上滑动，AD变成FD，如图（2）时，结论还成立吗？当它滑动到AE的延长线上时，AD变成FD，如图（3）时，结论还成立吗？证明你的结论．
10．小虫从某点O出发在一直线上来回爬行，若假定向右爬行的路程记为正数，向左爬行的路程记为负数，已知小虫爬行的路程依次记为：+5，-3，+10，-8，-6，+12，-10（单位：厘米），则：
（1）小虫最后回到出发点O了吗？若没有，在点O的什么地方？
（2）在爬行过程中，如果爬1厘米奖励两粒芝麻，则小虫一共得到多少粒芝麻？
11．菱形的面积为24，其中的一条较短的对角线长为6，则此菱形的周长为（　　）
A．24B．20C．12D．28

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网