题目内容
7.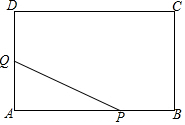 如图,在矩形ABCD中,AB=12cm,BC=9cm.P、Q两点同时从点B、D出发,分别沿BA、DA方向匀速运动(当P运动到A时,P、Q同时停止运动),已知P点的速度比Q点大1cm/s,设P点的运动时间为x秒,△PAQ的面积为ycm2,
如图,在矩形ABCD中,AB=12cm,BC=9cm.P、Q两点同时从点B、D出发,分别沿BA、DA方向匀速运动(当P运动到A时,P、Q同时停止运动),已知P点的速度比Q点大1cm/s,设P点的运动时间为x秒,△PAQ的面积为ycm2,(1)经过3秒△PAQ的面积是矩形ABCD面积的$\frac{1}{3}$时,求P、Q两点的运动速度分别是多少?
(2)以(1)中求出的结论为条件,写出y与x的函数关系式,并求出自变量x的取值范围.
分析 (1)设Q点的运动速度为vcm/s,则P的运动速度为(v+1)cm/s,得出DQ=3v,BP=3(v+1),根据3秒△PAQ的面积是矩形ABCD面积的$\frac{1}{3}$列出方程求解可得;
(2)根据题意知BP=(4-$\sqrt{2}$)x,DQ=(3-$\sqrt{2}$)x,由矩形面积公式可得函数解析式,根据AP≥0得出x的范围.
解答 解:(1)设Q点的运动速度为vcm/s,则P的运动速度为(v+1)cm/s,
则DQ=3v,BP=3(v+1),
由题意得:$\frac{1}{2}$•[12-3(v+1)]•(9-3v)=$\frac{1}{3}$×9×12,
解得:v=3+$\sqrt{2}$或v=3-$\sqrt{2}$,
又3(v+1)≤12,
∴v≤3,
∵3+$\sqrt{2}$>3,舍去,
故点Q的运动速度为3-$\sqrt{2}$cm/s,点P的运动速度为4-$\sqrt{2}$cm/s;
(2)当点Q的运动速度为3-$\sqrt{2}$cm/s,点P的运动速度为4-$\sqrt{2}$cm/s时,
BP=(4-$\sqrt{2}$)x,DQ=(3-$\sqrt{2}$)x,
∴y=$\frac{1}{2}$[12-(4-$\sqrt{2}$)x]•[9-(3-$\sqrt{2}$)x]
=$\frac{14-7\sqrt{2}}{2}$x2-$\frac{72-21\sqrt{2}}{2}$x+54,
∵9-(3-$\sqrt{2}$)x≥0,
∴0≤x≤$\frac{27+9\sqrt{2}}{7}$.
点评 本题主要考查二次函数的应用和一元二次方程的应用,根据题意表示出BP、DQ的长,由面积公式及相互间的相等关系列出方程或函数解析式是解题的关键.

 阅读快车系列答案
阅读快车系列答案 已知在Rt△ABC中,AC=BC,∠C=90°,D为边AB的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC、CB(或它们的延长线)于点E、F.
已知在Rt△ABC中,AC=BC,∠C=90°,D为边AB的中点,∠EDF=90°,∠EDF绕点D旋转,它的两边分别交AC、CB(或它们的延长线)于点E、F. 如图所示,AB为⊙O的直径,AB=6,∠CAD=30°,则弦DC=3.
如图所示,AB为⊙O的直径,AB=6,∠CAD=30°,则弦DC=3.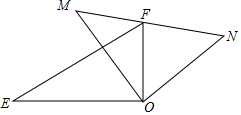 如图,一副三角板的两个直角顶点重合在一起.
如图,一副三角板的两个直角顶点重合在一起.