题目内容
17.解方程(组):(1)$\frac{1}{x-2}$+3=$\frac{1-x}{2-x}$;
(2)$\left\{\begin{array}{l}{3(x-5)=3y-6}\\{\frac{x-y}{3}=\frac{x+2y}{6}-2}\end{array}\right.$;
(3)x2-5(x-2)=5.
分析 (1)根据等式的性质,可得整式方程,根据解整式方程,可得方程的解;
(2)根据等式的性质,可化简方程组,根据加减校园法,可得方程组的解;
(3)根据公式法,可得方程的解.
解答 解:(1):(1)方程两边都乘以(x-2),得
1+3(x-2)=x-1.解得x=2,
检验:把x=2代入(x-2)=0,
∴x=2不是分式方程的解,
原分式方程无解;
(2)方程组化简,得$\left\{\begin{array}{l}{x-y=3①}\\{x-4y=-12②}\end{array}\right.$,
①-②,得
3y=15,
解得y=5,
把y=5代入①,得
x-5=-3,
解得x=2
原方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$;
(3)x2-5x+5=0,
a=1,b=-5,c=5,△=b2-4ac=(-5)2-4×1×5=5>0,
x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{5±\sqrt{5}}{2}$,
x1=$\frac{5+\sqrt{5}}{2}$,x2=$\frac{5-\sqrt{5}}{2}$.
点评 本题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解,解分式方程一定注意要验根;(2)利用了加减校园法解方程组;(3)利用公式法解一元二次方程,要把方程化成一般形式.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
7.为了鼓励居民节约用水,某市自来水公司对每户月用水量进行计费,每户每月用水量在规定吨数以下的收费标准相同;规定吨数以上的超过部分收费标准相同,以下是小明家1-5月份用水量和缴费情况:
根据表格中提供的信息,回答以下问题:
(1)求出规定吨数和两种收费标准.
(2)若小明家6月份用水20吨,则应缴多少元?
(3)若小明家7月份缴水费100元,则7月份用水多少吨?
| 月份 | 1 | 2 | 3 | 4 | 5 |
| 用水量(吨) | 8 | 10 | 13 | 15 | 18 |
| 费 用(元) | 16 | 20 | 29 | 35 | 44 |
(1)求出规定吨数和两种收费标准.
(2)若小明家6月份用水20吨,则应缴多少元?
(3)若小明家7月份缴水费100元,则7月份用水多少吨?
5.将20个数据各减去30后,得到的一组新数据的平均数是6,则这20个数据的平均数是( )
| A. | 35 | B. | 36 | C. | 37 | D. | 38 |
7.在一个不透明的口袋中装有6个完全相同的小球,把它们分别标号为1,2,3,4,5,6,从中随机摸出一个小球,其标号大于2的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
 如图,已知△ABC和△DEF是全等的等边三角形,且它们的重合部分是等边三角形ABC的一半,求证:△AGI是等边三角形.
如图,已知△ABC和△DEF是全等的等边三角形,且它们的重合部分是等边三角形ABC的一半,求证:△AGI是等边三角形.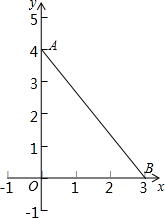 如图,在平面直角坐标系中有一条线段AB,其中A(0,4),B(3,0).请你在坐标轴上找一点P,使△ABP是等腰三角形.你能找到多少符合条件的点P?在图上标出所有的点P,并写出P点的坐标.
如图,在平面直角坐标系中有一条线段AB,其中A(0,4),B(3,0).请你在坐标轴上找一点P,使△ABP是等腰三角形.你能找到多少符合条件的点P?在图上标出所有的点P,并写出P点的坐标.