题目内容
2.关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a、b、c分别为△ABC三边的长.(1)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由;
(2)如果△ABC是等边三角形,试求这个一元二次方程的根.
分析 (1)利用根的判别式进而得出关于a,b,c的等式,进而判断△ABC的形状;
(2)利用△ABC是等边三角形,则a=b=c,进而代入方程求出即可.
解答 解:(1)∵方程有两个相等的实数根,
∴(2b)2-4(a+c)(a-c)=0,
∴4b2-4a2+4c2=0,
∴a2=b2+c2,
∴△ABC是直角三角形;
(2)∵当△ABC是等边三角形,
∴a=b=c,
∵(a+c)x2+2bx+(a-c)=0,
∴2ax2+2ax=0,
∴x1=0,x2=-1.
点评 此题主要考查了一元二次方程的应用以及根的判别式和勾股定理逆定理等知识,正确由已知获取等量关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知函数:①y=3x-1;②y=3x2-1;③y=-20x2;④y=x2-6x+5,其中是二次函数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.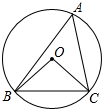 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
 如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )
如图,⊙O是△ABC的外接圆,∠BOC=100°,则∠A的度数等于( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |