题目内容
16.$\frac{\sqrt{3-x}}{\sqrt{x+1}}$=$\sqrt{\frac{3-x}{x+1}}$成立的条件是( )| A. | x≥-1 | B. | x≤3 | C. | -1≤x≤3 | D. | -1<x≤3 |
分析 根据二次根式的性质分别得出关于x的不等式进而求出答案.
解答 解:∵$\frac{\sqrt{3-x}}{\sqrt{x+1}}$=$\sqrt{\frac{3-x}{x+1}}$成立,
∴$\left\{\begin{array}{l}{3-x≥0}\\{x+1>0}\end{array}\right.$,
解得:-1<x≤3.
故选:D.
点评 此题主要考查了二次根式的性质,正确正确二次根式有意义的条件是解题关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
11.下列图案中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.若mn>0,则m,n( )
| A. | m,n一定是正数 | B. | m,n一定是负数 | C. | m,n一定是同号 | D. | m,n一定是异号 |
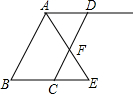 如图,已知AB∥CD,AE平分∠BAD,CD与AE相交于点F.
如图,已知AB∥CD,AE平分∠BAD,CD与AE相交于点F.