题目内容
4.矩形ABCD中,AB=3,BC=5.E位CD边上一点,将矩形沿直线BE折叠.(1)使点C落在AD边上,求DE的长.
(2)使点C落在线段BD上C′处,求DE的长.
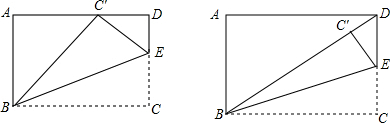
分析 (1)由折叠可得BC′=BC=5,EC′=EC,根据勾股定理求出AC′,即可求出C′D,设DE=x,则C′E=CE=3-x,然后在Rt△C′DE中运用勾股定理,就可解决问题;
(2)可根据勾股定理求出BD,由折叠可得BC′=BC=5,EC′=EC,∠BC′E=∠C=90°,从而求出C′D,设DE=x,则C′E=CE=3-x,然后在Rt△C′DE中运用勾股定理,就可解决问题.
解答 解:(1)由折叠可得BC′=BC=5,EC′=EC.
∵四边形ABCD是矩形,
∴∠A=∠D=90°,DC=AB=3,AD=BC=5,
∴AC′=4,C′D=1.
设DE=x,则C′E=CE=3-x.
在Rt△C′DE中,
(3-x)2=x2+12,
解得x=$\frac{4}{3}$,
∴DE的长为$\frac{4}{3}$;
(2)∵四边形ABCD是矩形,
∴∠A=∠C=90°,DC=AB=3,AD=BC=5,
∴BD=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$.
由折叠可得BC′=BC=5,EC′=EC,∠BC′E=∠C=90°,
∴C′D=$\sqrt{34}$-5,∠DC′E=90°
设DE=x,则C′E=CE=3-x.
在Rt△C′DE中,
x2=(3-x)2+($\sqrt{34}$-5)2,
解得x=$\frac{34-5\sqrt{34}}{3}$,
∴DE的长为$\frac{34-5\sqrt{34}}{3}$.
点评 本题主要考查了矩形的性质、轴对称的性质、勾股定理等知识,关于矩形的折叠问题,通常是转化到一个直角三角形中,运用勾股定理来解决.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
16.$\frac{\sqrt{3-x}}{\sqrt{x+1}}$=$\sqrt{\frac{3-x}{x+1}}$成立的条件是( )
| A. | x≥-1 | B. | x≤3 | C. | -1≤x≤3 | D. | -1<x≤3 |
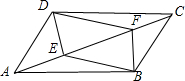 如图,在?ABCD中,E,F是对角线AC上两点
如图,在?ABCD中,E,F是对角线AC上两点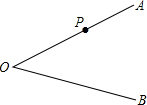 如图,已知∠AOB,点P在射线OA上.
如图,已知∠AOB,点P在射线OA上.