题目内容
8.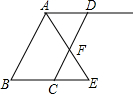 如图,已知AB∥CD,AE平分∠BAD,CD与AE相交于点F.
如图,已知AB∥CD,AE平分∠BAD,CD与AE相交于点F.(1)若∠CFE=∠E,则AD与BE平行吗?判断并说明理由;
(2)若∠CFE=∠DCE,则∠ADC与∠E相等吗?判断并说明理由.
分析 根据两直线平行,内错角相等可得∠CFE=∠BAE,根据角平分线的定义可得∠BAE=∠DAE,从而得到∠CFE=∠DAE;
(1)求出∠DAE=∠E,然后根据内错角相等,两直线平行证明即可;
(2)求出∠DAE=∠AFD=∠CFE=∠DCE,再根据三角形的内角和定理求解即可.
解答 解:∵AB∥CD,
∴∠CFE=∠BAE,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠CFE=∠DAE,
(1)AD∥BE.
理由如下:∵∠CFE=∠E,
∴∠DAE=∠E,
∴AD∥BE;
(2)∠ADC=∠E.
理由如下:∵∠CFE=∠AFD(对顶角相等),
∴∠DAE=∠AFD,
又∵∠CFE=∠DCE,
∴∠DAE=∠AFD=∠CFE=∠DCE,
在△ADF中,∠ADC=180°-∠DAE-∠AFD,
在△CEF中,∠E=180°-∠CFE-∠DCE,
∴∠ADC=∠E.
点评 本题考查了平行线的判定与性质,三角形的内角和定理,熟记平行线的性质与判定方法并准确识图,理清图中各角度之间的关系是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.$\frac{\sqrt{3-x}}{\sqrt{x+1}}$=$\sqrt{\frac{3-x}{x+1}}$成立的条件是( )
| A. | x≥-1 | B. | x≤3 | C. | -1≤x≤3 | D. | -1<x≤3 |
 如图,在四边形ABCD中,AB=3cm,CD=2cm,∠BAD=60°,∠CDA=∠CBA=90°,求四边形ABCD的面积.
如图,在四边形ABCD中,AB=3cm,CD=2cm,∠BAD=60°,∠CDA=∠CBA=90°,求四边形ABCD的面积. 如图,已知∠AOB,点P在射线OA上.
如图,已知∠AOB,点P在射线OA上.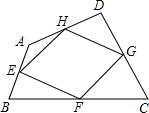 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,请添加一个与四边形ABCD对角线有关的条件,为AC⊥BD,使四边形EFGH是矩形.
如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,请添加一个与四边形ABCD对角线有关的条件,为AC⊥BD,使四边形EFGH是矩形.