题目内容
20.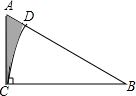 如图,△ABC中,∠ACB=90°,AB=2AC=6,以B为圆心BC为半径作弧交AB于点D,则阴影部分的面积为$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.
如图,△ABC中,∠ACB=90°,AB=2AC=6,以B为圆心BC为半径作弧交AB于点D,则阴影部分的面积为$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.
分析 先根据锐角三角函数的定义求出∠B的度数,再由勾股定理求出BC的长,再根据S阴影=S△ABC-S扇形BCD进行解答即可.
解答 解:∵∠ACB=90°,AB=2AC=6,
∴AC=3,∠B=30°,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=3$\sqrt{3}$,
∴S阴影=S△ABC-S扇形BCD=$\frac{1}{2}$AC•BC-$\frac{30π•B{C}^{2}}{360}$=$\frac{1}{2}×3×3\sqrt{3}$-$\frac{30π×(3\sqrt{3})^{2}}{360}$=$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.
故答案为:$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.
点评 本题考查的是扇形面积的计算及直角三角形的性质,熟知三角形及扇形的面积公式是解答此题的关键.

练习册系列答案
相关题目

 如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).用一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-B…的规律紧绕在四边形ABCD的边上.
如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).用一条长为a个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D-A-B…的规律紧绕在四边形ABCD的边上. 在△ABC中,∠C=∠ABC,AE∥BC,BE平分∠ABC,则下列结论中一定成立的是①②④(把所有正确结论的序号都填在横线上).
在△ABC中,∠C=∠ABC,AE∥BC,BE平分∠ABC,则下列结论中一定成立的是①②④(把所有正确结论的序号都填在横线上).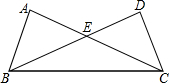 如图,在Rt△ABC和Rt△BCD中,∠A=∠D=90°,AB=CD=4,BC=$4\sqrt{5}$,△BCE的面积=10.
如图,在Rt△ABC和Rt△BCD中,∠A=∠D=90°,AB=CD=4,BC=$4\sqrt{5}$,△BCE的面积=10.