题目内容
5.为了求1+2+22+23+…+22010的值,可令S=1+2+22+23+…+22010,则2S=2+22+23+24+…+22011,因此2S-S=22011-1,所以1+2+22+23+…+22010=22011-1,仿照以上推理,计算1+3+32+33+…+3333的值可得$\frac{{3}^{334}-1}{2}$.分析 仿照题中的方法,设原式=S,两边乘以3变形后相减即可求出值.
解答 解:令S=1+3+32+33+…+3333,
则3S=3+32+33+…+3334,
因此3S-S=3334-1,即S=$\frac{{3}^{334}-1}{2}$,
则1+3+32+33+…+3333=$\frac{{3}^{334}-1}{2}$,
故答案为:$\frac{{3}^{334}-1}{2}$
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
13.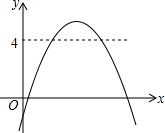 已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )
已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )
 已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )
已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )| A. | 有两个不相等的正实数根 | B. | 有两个异号实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
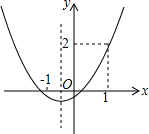 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③a<$\frac{1}{2}$;④b>1.其中正确的结论是②④.
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③a<$\frac{1}{2}$;④b>1.其中正确的结论是②④.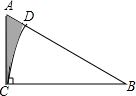 如图,△ABC中,∠ACB=90°,AB=2AC=6,以B为圆心BC为半径作弧交AB于点D,则阴影部分的面积为$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.
如图,△ABC中,∠ACB=90°,AB=2AC=6,以B为圆心BC为半径作弧交AB于点D,则阴影部分的面积为$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.