题目内容
10.已知:关于x的方程x2+4x+(2-k)=0有两个不相等的实数根.(1)求实数k的取值范围.
(2)取一个k的负整数值,且求出这个一元二次方程的根.
分析 (1)因为方程有两个不相等的实数根,△>0,由此可求k的取值范围;
(2)在k的取值范围内,取负整数,代入方程,解方程即可.
解答 解:(1)∵方程x2+4x+(2-k)=0有两个不相等的实数根,
∴42-4(2-k)>0,
即4k+8>0,解得k>-2;
(2)若k是负整数,k只能为-1;
如果k=-1,原方程为x2+4x+3=0,
解得:x1=-1,x2=-3.
点评 此题考查一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
相关题目
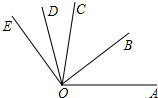 如图,OB是∠A0C的平分线,OD是∠COE的平分线.
如图,OB是∠A0C的平分线,OD是∠COE的平分线.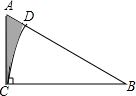 如图,△ABC中,∠ACB=90°,AB=2AC=6,以B为圆心BC为半径作弧交AB于点D,则阴影部分的面积为$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.
如图,△ABC中,∠ACB=90°,AB=2AC=6,以B为圆心BC为半径作弧交AB于点D,则阴影部分的面积为$\frac{9\sqrt{3}}{2}$-$\frac{9π}{4}$.